初中数学苏科版九年级下册 6.7 用相似三角形解决问题 同步训练
试卷更新日期：2021-03-04 类型：同步测试
一、单选题
-
1. 在相同时刻物高与影长成比例，如果高为1.5m的测竿的影长为 2.5m，那么影长为30m的旗杆的高度是（ ）
A、20m B、16m C、18m D、15m2. 一个三角形木架三边长分别是75cm，100cm，120cm，现要再做一个与其相似的三角形木架，而只有长为60cm和120cm的两根木条.要求以其中一根为一边，从另一根截下两段作为另两边（允许有余料），则不同的截法有（ ）A、一种 B、两种 C、三种 D、四种3. 如图，一同学在湖边看到一棵树，他目测出自己与树的距离为20m，树的顶端在水中的倒影距自己5m 远，该同学的身高为1.7m ，则树高为（ ）.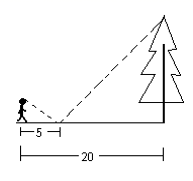
A、3.4m B、4.7 m C、5.1m D、6.8m4. 如图，身高1.5米的小西站在点D处，此时路灯M照射的影子AD为2.5米，小西沿着 的方向行走4.5米至点F，此时影子 为1米，则路灯BM的高度为（ ）
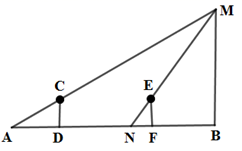A、3米 B、3.5米 C、4.5米 D、6米5. 一张等腰三角形纸片，底边长15cm，底边上的高长22.5cm，现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条，如图所示，已知剪得的纸条中有一张是正方形，则这张正方形纸条是（ ）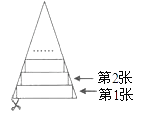
A、第4张 B、第5张 C、第6张 D、第7张6. 如图，锐角三角形 ，边 ，高 ，其内接的正方形的一边在 上，其余两个顶点分别在 ， 上，则正方形的边长 为（ ）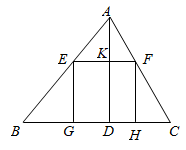
A、2.6 B、2.4 C、3 D、1.27. 如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD＝12 m，塔影长DE＝18 m，小明和小华的身高都是1.6m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，那么塔高AB为（ ）
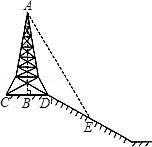A、24m B、22m C、20m D、18m8. 如图所示，某超市在一楼至二楼之间安装有电梯，天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过，请你根据图中数据回答，两层楼之间的高约为（ ）
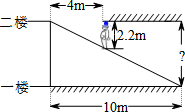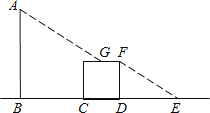
A、 B、 C、11m D、9.如图，路边有一根电线杆AB和一块正方形广告牌（不用考虑牌子的厚度）．有一天，小明突然发现，在太阳光照射下，电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处，而正方形广告牌的影子刚好落在地面上E点，已知BC=5米，正方形边长为2米，DE=4米．则此时电线杆的高度是（ ）米．
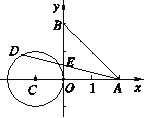
A、8 B、7 C、6 D、510.如图，在平面直角坐标系xOy中，A(2，0)，B(0，2)，⊙C的圆心为点C(-1，0)，半径为1．若D是⊙C上的一个动点，线段DA与y轴交于点E ， 则△ABE面积的最小值是（ ）
A、2 B、 C、 D、二、填空题
-
11. 如图，为估算某河的宽度，在河对岸选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上．若测得BE＝20m，CE＝10m，CD＝20m，则河的宽度AB等于m
12. 如图，身高为1.8米的某学生想测量学校旗杆的高度，当他站在B处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AB=2米，BC=18米，则旗杆CD的高度是米．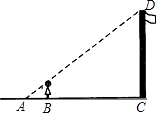
13. 如图是圆桌正上方的灯泡O发出的光线照射桌面后，在地面上形成阴影（圆形）的示意图．已知桌面的直径为1.2m，桌面距离地面1m，若灯泡O距离地面3m，则地面上阴影部分的面积为m2 ．
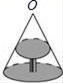14. 相邻两根电杆都用钢索在地面上固定，如图，一根电杆钢索系在离地面4米处，另一根电杆钢索系在离地面6米处，两根电线杆的钢索都有一根固定在另一根电线杆底部，则中间两根钢索相交处点P离地面米
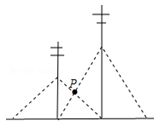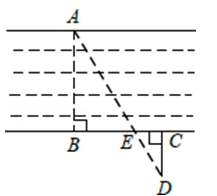
15. 如图，一电线杆 的影子分别落在了地上和墙上．同一时刻，小明竖起 米高的直杆 ，量得其影长 为 米，量得电线杆 落在地上的影子 长 米，落在墙上的影子 的高为 米，则电线杆 的高为米．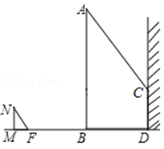
16. 如图，阳光通过窗口照到室内，在地面上留下1.6m宽的亮区DE ， 已知亮区一边到窗下的墙脚距离CE=3.6m，窗高AB=1.2m，那么窗口底边离地面的高度BC=m．
17. 如图1，长、宽均为3高为8的长方体容器，放置在水平桌面上，里面盛有水，水面高为6，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图2是此时的示意图，则图2中水面高度为 ．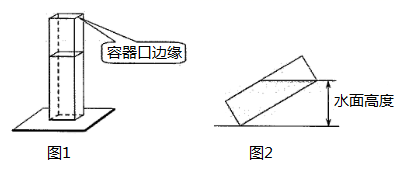
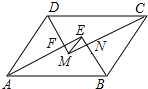
18.如图，▱ABCD中，AB＞AD，AE，BE，CM，DM分别为∠DAB，∠ABC，∠BCD，∠CDA的平分线，AE与DM相交于点F，BE与CM相交于点N，连接EM．若▱ABCD的周长为42cm，FM=3cm，EF=4cm，则EM= cm，AB= cm．
三、解答题
-
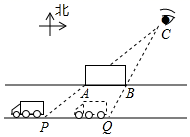
19. 某天，小芳走到如图所示的C处时，看到正对面一条东西走向的笔直公路.上有一辆汽车从东面驶来，到达Q处时，恰好被公路北侧边上竖着的一个长12m的广告牌AB挡住，3s后在P处又重新看到该汽车的全部车身，已知该汽车的行驶速度是6m/s，假设AB PQ，公路宽为10m，求小芳所在C处到公路南侧PQ的距离.
20. 在一次数学活动课上，小芳到操场上测量旗杆的高度，她的测量方法是：拿一根高3.5米的竹竿直立在离旗杆27米的C处（如图），然后沿BC方向走到D处，这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上，又测得C、D两点的距离为3米，小芳的目高为1.5米，利用她所测数据，求旗杆的高.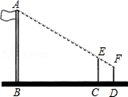
21. 如图，小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上.已知纸板的两条直角边 ， ，测得 ，边DF离地面的高度 ，求树高AB.
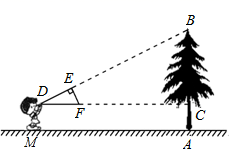22. 如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙上的影高为2米，求旗杆的高度．
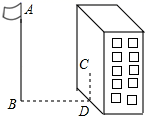23. 李师傅用镜子测量一棵古树的高，但树旁有一条小河，不便测量镜子与树之间的距离，于是他两次利用镜子，第一次把镜子放在C点（如图所示），人在F点正好在镜中看到树尖A；第二次他把镜子放在 处，人在 处正好看到树尖A.已知李师傅眼睛距地面的高度为 ，量得 为 ， 为 ， 为 ，求树高.
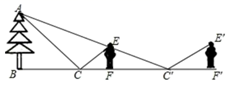24. 学习了相似三角形的知识后，爱探究的小明下晚自习后利用路灯的光线去测量了一路灯的高度，并作出了示意图：如图，路灯（点P）距地面若干米，身高1.6米的小明站在距路灯的底部（O点）20米的A点时，身影的长度AM为5米；
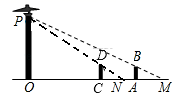(1)、请帮助小明求出路灯距地面的高度；(2)、若另一名身高为1.5米小龙站在直线OA上的C点时，测得他与小明的距离AC为7米，求小龙的身影的长度．25. 如图，灯杆AB与墙MN的距离为18米，小丽在离灯杆（底部）9米的D处测得其影长DF为3m，设小丽身高为1.6m.
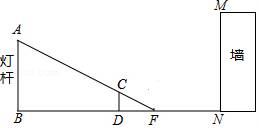(1)、求灯杆AB的高度；(2)、小丽再向墙走7米，她的影子能否完全落在地面上？若能，求此时的影长；若不能，求落在墙上的影长.26. 如图，AB和DE直立在地面上的两根立柱，已知AB=5m，某一时刻AB在太阳光下的影子长BC=3m.
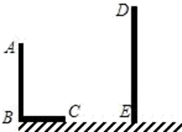(1)、在图中画出此时DE在太阳光下的影子EF；(2)、在测量AB影子长时，同时测量出EF=6m，计算DE的长.27. 如图1，在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，AB=4.若△ABC固定不动，△AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合，点E不与点C重合).
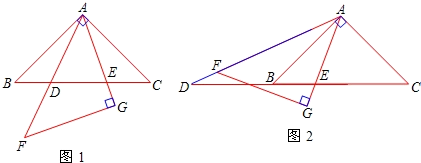(1)、求证：△ABE∽△DCA；(2)、若BE·CD=k（k为常数），求k的值；(3)、在旋转过程中，当△AFG旋转到如图2的位置时，AG与BC交于点E，AF的延长线与CB的延长线交于点D，那么（2）中k的值是否发生了变化?为什么?28. 已知菱形ABCD中，∠ABC=60°，AB=4，点M在BC边上，过点M作PM∥AB交对角线BD于点P，连接PC.
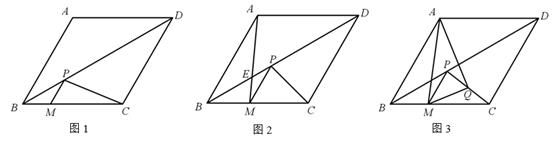(1)、如图1，当BM=1时，求PC的长；(2)、如图2，设AM与BD交于点E，当∠PCM=45°时，求证： = ；(3)、如图3，取PC的中点Q，连接MQ，AQ.①请探究AQ和MQ之间的数量关系，并写出探究过程；
②△AMQ的面积有最小值吗？如果有，请直接写出这个最小值；如果没有，请说明理由.