初中数学苏科版九年级下册6.6 图形的位似 同步训练
试卷更新日期:2021-03-04 类型:同步测试
一、单选题
-
1. 若两个图形位似,则下列叙述不正确的是( )A、每对对应点所在的直线相交于同一点 B、两个图形上的对应线段之比等于位似比 C、两个图形上的对应线段必平行 D、两个图形的面积比等于位似比的平方2. 下列图形中不是位似图形的为( )A、
 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为0.5,把△EFO缩小,则点E的对应点E′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣2,1)或(2,﹣1) D、(﹣8,4)或(8,﹣4)4. 如图,四边形ABCD和四边形A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,四边形ABCD的面积等于4,则四边形A′B′C′D′的面积为( )
3. 在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为0.5,把△EFO缩小,则点E的对应点E′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣2,1)或(2,﹣1) D、(﹣8,4)或(8,﹣4)4. 如图,四边形ABCD和四边形A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,四边形ABCD的面积等于4,则四边形A′B′C′D′的面积为( ) A、3 B、4 C、6 D、95. 已知A(0,-1),B(1,-3),先将线段AB向左平移3个单位,再以原点O为位似中心,在第一象限内,将其扩大为原来3倍,则点A的对应点坐标为( )A、(3,9) B、(6,3) C、(6,9) D、(9,3)6. 在平面直角坐标系中,矩形 的顶点坐标分别是 , , , .已知矩形 与矩形 位似,位似中心是原点 ,且矩形 的面积等于矩形 面积的 ,则点 的坐标为( )A、 B、 或 C、 D、 或7. 如图,线段AB两个端点坐标分别为A(6,9),B(9,3),以原点O为位似中心,在第三象限内将线段AB缩小为原来的 后,得到线段CD,则点C的坐标为( )
A、3 B、4 C、6 D、95. 已知A(0,-1),B(1,-3),先将线段AB向左平移3个单位,再以原点O为位似中心,在第一象限内,将其扩大为原来3倍,则点A的对应点坐标为( )A、(3,9) B、(6,3) C、(6,9) D、(9,3)6. 在平面直角坐标系中,矩形 的顶点坐标分别是 , , , .已知矩形 与矩形 位似,位似中心是原点 ,且矩形 的面积等于矩形 面积的 ,则点 的坐标为( )A、 B、 或 C、 D、 或7. 如图,线段AB两个端点坐标分别为A(6,9),B(9,3),以原点O为位似中心,在第三象限内将线段AB缩小为原来的 后,得到线段CD,则点C的坐标为( ) A、 B、 C、 D、8. 如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x , y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )
A、 B、 C、 D、8. 如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x , y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( ) A、(﹣x , ﹣y) B、(﹣2x , ﹣2y) C、(﹣2x , 2y) D、(2x , ﹣2y)9. 如图,网格中的两个三角形是位似图形,它们的位似中心是( )
A、(﹣x , ﹣y) B、(﹣2x , ﹣2y) C、(﹣2x , 2y) D、(2x , ﹣2y)9. 如图,网格中的两个三角形是位似图形,它们的位似中心是( ) A、点A B、点B C、点C D、点D10. 如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点 A' , , .下列说法正确的是( )
A、点A B、点B C、点C D、点D10. 如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点 A' , , .下列说法正确的是( )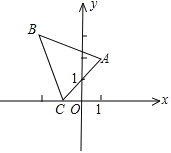 A、△ 与△ABC是位似图形,位似中心是点(1,0) B、△ 与△ABC是位似图形,位似中心是点(0,0) C、△ 与△ABC是相似图形,但不是位似图形 D、△ 与△ABC不是相似图形
A、△ 与△ABC是位似图形,位似中心是点(1,0) B、△ 与△ABC是位似图形,位似中心是点(0,0) C、△ 与△ABC是相似图形,但不是位似图形 D、△ 与△ABC不是相似图形二、填空题
-
11. 如图,以点O为位似中心,将 放大后得到 , ,则 .
 12. 如图,已知线段AB两个端点的坐标分别为A(4,6),B(8,4),以原点O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段CD , 则端点D坐标为 .
12. 如图,已知线段AB两个端点的坐标分别为A(4,6),B(8,4),以原点O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段CD , 则端点D坐标为 .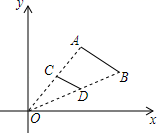 13. 在平面直角坐标系中,点A的坐标是 ,以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为 .若点 恰在某一反比例函数图象上,则该反比例函数的解析式为 .14. 如图,平面直角坐标系中有正方形 和正方形 ,若点 和点 的坐标分别为 , ,则两个正方形的位似中心的坐标是 .
13. 在平面直角坐标系中,点A的坐标是 ,以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为 .若点 恰在某一反比例函数图象上,则该反比例函数的解析式为 .14. 如图,平面直角坐标系中有正方形 和正方形 ,若点 和点 的坐标分别为 , ,则两个正方形的位似中心的坐标是 .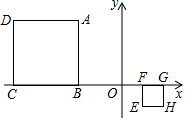 15. 如图, 是 内任意一点, 分别为 上的点,且 与 是位似三角形,位似中心为 .若 则 与 的位似比为.
15. 如图, 是 内任意一点, 分别为 上的点,且 与 是位似三角形,位似中心为 .若 则 与 的位似比为. 16. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,两个矩形在O的同侧,且矩形OA'B'C'的面积等于矩形OABC面积的 ,那么点B'的坐标是.
16. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,两个矩形在O的同侧,且矩形OA'B'C'的面积等于矩形OABC面积的 ,那么点B'的坐标是. 17. 如图,在平面直角坐标系中,已知A(1.5,0),D(4.5,0),△ABC与△DEF位似,原点O是位似中心.若DE=7.5,则AB= .
17. 如图,在平面直角坐标系中,已知A(1.5,0),D(4.5,0),△ABC与△DEF位似,原点O是位似中心.若DE=7.5,则AB= . 18. 如图,直线y= x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为 .
18. 如图,直线y= x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为 .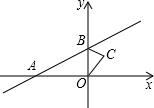
三、解答题
-
19. 如图,△ABC中,AD、BE是高.
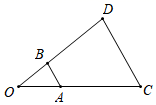
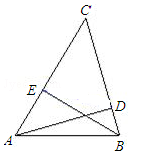 (1)、求证:;(2)、连接DE,那么△CDE与△CAB是位似图形吗?20. 如图, OAB与 ODC是位似图形 。
(1)、求证:;(2)、连接DE,那么△CDE与△CAB是位似图形吗?20. 如图, OAB与 ODC是位似图形 。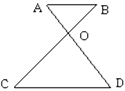
试问:
(1)、AB与CD平行吗?请说明理由 。(2)、如果OB=3,OC=4,OD=3.5.试求 OAB与 ODC的相似比及OA的长 。21. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①以O为位似中心在第二象限作位似比为1:2变换,得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标;
②以原点O为旋转中心,画出把△ABC顺时针旋转90°的图形△A2B2C2 , 并写出C2的坐标.
22. 如图,已知A (﹣4,2),B (﹣2,6),C (0,4)是直角坐标系平面上三点. (1)、把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1 , 画出平移后的图形;(2)、若△ABC内部有一点P (a,b),则平移后它的对应点Pl的坐标为;(3)、以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2 , 请在所给的坐标系中作出所有满足条件的图形.23.
(1)、把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1 , 画出平移后的图形;(2)、若△ABC内部有一点P (a,b),则平移后它的对应点Pl的坐标为;(3)、以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2 , 请在所给的坐标系中作出所有满足条件的图形.23.如图在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(﹣2,4),B(﹣2,1),C(﹣5,2).
 (1)、画出△ABC关于x轴对称的△A1B1C1;(2)、将△A1B1C1的三个顶点的横坐标与纵坐同时乘以﹣2,得到对应的点A2 , B2 , C2 , 请画出△A2B2C2;(3)、则S△A1B1C1:S△A2B2C2 .24. 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)、画出△ABC关于x轴对称的△A1B1C1;(2)、将△A1B1C1的三个顶点的横坐标与纵坐同时乘以﹣2,得到对应的点A2 , B2 , C2 , 请画出△A2B2C2;(3)、则S△A1B1C1:S△A2B2C2 .24. 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
①将△ABC绕点A顺时针旋转90°后得到△AB1C1 , 在图①中画出△AB1C1 , 并求出在旋转过程中△ABC
扫过的面积;
②在图②中以点O为位似中心,将△ABC缩小为原来的 ,并写出点C的对应点的坐标.
25. 如图所示,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上. (1)、若点F的坐标为(6,3),直接写出点C和点A的坐标;(2)、若正方形BEFG的边长为6,求点C的坐标.26. 如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2 , b1≠b2 , 那么称这两个一次函数为“平行一次函数”.
(1)、若点F的坐标为(6,3),直接写出点C和点A的坐标;(2)、若正方形BEFG的边长为6,求点C的坐标.26. 如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2 , b1≠b2 , 那么称这两个一次函数为“平行一次函数”.如图,已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”
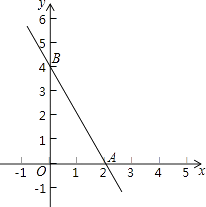 (1)、若函数y=kx+b的图象过点(3,1),求b的值;(2)、若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.27. 如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)、若函数y=kx+b的图象过点(3,1),求b的值;(2)、若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.27. 如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程) (1)、如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;(2)、如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.28. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,3).且点A的坐标为(﹣1,0),点B的坐标为(3,0),点P是抛物线上第一象限内的一个点.
(1)、如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;(2)、如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.28. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,3).且点A的坐标为(﹣1,0),点B的坐标为(3,0),点P是抛物线上第一象限内的一个点. (1)、求抛物线的函数表达式;(2)、连PO、PB,如果把△POB沿OB翻转,所得四边形POP′B恰为菱形,那么在抛物线的对称轴上是否存在点Q,使△QAB与△POB相似?若存在求出点Q的坐标;若不存在,说明理由;(3)、若(2)中点Q存在,指出△QAB与△POB是否位似?若位似,请直接写出其位似中心的坐标.
(1)、求抛物线的函数表达式;(2)、连PO、PB,如果把△POB沿OB翻转,所得四边形POP′B恰为菱形,那么在抛物线的对称轴上是否存在点Q,使△QAB与△POB相似?若存在求出点Q的坐标;若不存在,说明理由;(3)、若(2)中点Q存在,指出△QAB与△POB是否位似?若位似,请直接写出其位似中心的坐标.