初中数学苏科版九年级下册6.4 探索三角形相似的条件 同步训练
试卷更新日期:2021-03-04 类型:同步测试
一、单选题
-
1. 下列判断中,错误的有( )A、三边对应成比例的两个三角形相似 B、两边对应成比例,且有一个角相等的两个三角形相似 C、有一个锐角相等的两个直角三角形相似 D、有一个角是100°的两个等腰三角形相似2. 如图,已知 ,那么下列结论正确的是( )
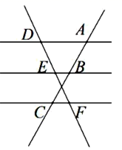 A、 B、 C、 D、3. 已知△ABC中,D , E分别是边BC , AC上的点,下列各式中,不能判断DE∥AB的是( )A、 B、 C、 D、4. 如图,D为△ABC边BC上一点,要使△ABD∽△CBA,应该具备下列条件中的( )
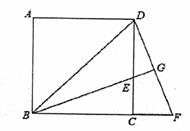
A、 B、 C、 D、3. 已知△ABC中,D , E分别是边BC , AC上的点,下列各式中,不能判断DE∥AB的是( )A、 B、 C、 D、4. 如图,D为△ABC边BC上一点,要使△ABD∽△CBA,应该具备下列条件中的( ) A、 B、 C、 D、5. 下列条件中,不能判断△ABC与△DEF相似的是( )A、∠A=∠D , ∠B=∠F B、 且∠B=∠D C、 D、 且∠A=∠D6. 如图所示,在▱ABCD.BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有( )
A、 B、 C、 D、5. 下列条件中,不能判断△ABC与△DEF相似的是( )A、∠A=∠D , ∠B=∠F B、 且∠B=∠D C、 D、 且∠A=∠D6. 如图所示,在▱ABCD.BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有( )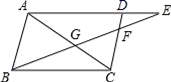 A、3对 B、4对 C、5对 D、6对7. 如图,网格中有一个△ABC,下图中与△ABC相似的三角形的个数有( )
A、3对 B、4对 C、5对 D、6对7. 如图,网格中有一个△ABC,下图中与△ABC相似的三角形的个数有( )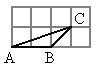

 A、1个 B、2个 C、3个 D、4个8. 如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
A、1个 B、2个 C、3个 D、4个8. 如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )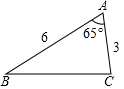 A、
A、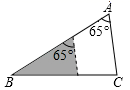 B、
B、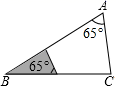 C、
C、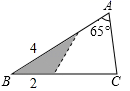 D、
D、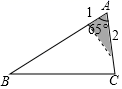 9. 如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )
9. 如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )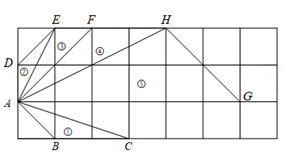 A、②④ B、②⑤ C、③④ D、④⑤10. 如图所示,下列条件中能单独判断△ABC∽△ACD的个数是( )个.
A、②④ B、②⑤ C、③④ D、④⑤10. 如图所示,下列条件中能单独判断△ABC∽△ACD的个数是( )个.①∠ABC=∠ACD;②∠ADC=∠ACB;③ = ;④AC2=AD•AB
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,当∠AED=时,△ADE与△ABC相似.
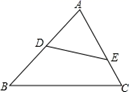 12. 如图,已知 ,请添加一个条件,使 ,这个条件可以是.
12. 如图,已知 ,请添加一个条件,使 ,这个条件可以是. 13. 如图,AB∥CD∥EF,点C,D分别在BE,AF上,如果BC=4,CE=6,AF=8,那么DF的长.
13. 如图,AB∥CD∥EF,点C,D分别在BE,AF上,如果BC=4,CE=6,AF=8,那么DF的长.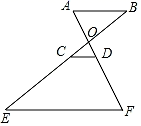 14. 如图,在△ABC中,∠C=90°,BC=16 cm,AC=12 cm,点P从点B出发,沿BC以2 cm/s的速度向点C移动,点Q从点C出发,以1 cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为ts,当t=时,△CPQ与△CBA相似.
14. 如图,在△ABC中,∠C=90°,BC=16 cm,AC=12 cm,点P从点B出发,沿BC以2 cm/s的速度向点C移动,点Q从点C出发,以1 cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为ts,当t=时,△CPQ与△CBA相似.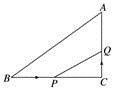 15. 如图,已知△ABC.D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为时,△ADP和△ABC相似.
15. 如图,已知△ABC.D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为时,△ADP和△ABC相似.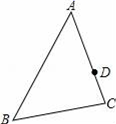 16. 如图,在△ABC中, 是边AB的中点,过点O的直线l将△ABC分割成两个部分,若其中的一个部分与△ABC相似,则满足条件的直线l共有条.
16. 如图,在△ABC中, 是边AB的中点,过点O的直线l将△ABC分割成两个部分,若其中的一个部分与△ABC相似,则满足条件的直线l共有条.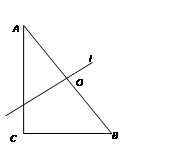 17. 如图,AD∥BC,∠D=90°,AD=2,BC=6,DC=8,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有个.
17. 如图,AD∥BC,∠D=90°,AD=2,BC=6,DC=8,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有个.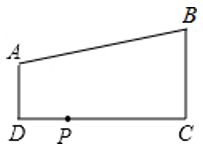 18. 如图是一个量角器和一个含30°的直角三角板放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半面O于点F,且BC=OE=2.若以O、B、F为顶点的三角形与△ABC相似,则OB的长为.
18. 如图是一个量角器和一个含30°的直角三角板放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半面O于点F,且BC=OE=2.若以O、B、F为顶点的三角形与△ABC相似,则OB的长为.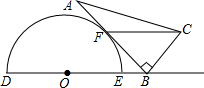 19. 如图,点G是△ABC的重心,GH⊥BC,垂足为点H,若GH=2.5,则点A到BC的距离为.
19. 如图,点G是△ABC的重心,GH⊥BC,垂足为点H,若GH=2.5,则点A到BC的距离为.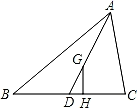
三、解答题
-
20. 如图,D、E分别是△ABC的边AB、AC上的点,AB=9,BD=7,AC=6,CE=3,求证:△ADE∽△ACB.
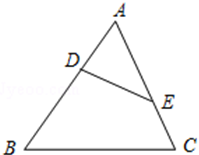 21. 如图,在等边三角形ABC中,点E,D分别在BC,AB上,且∠AED=60°,求证:△AEC~△EDB.
21. 如图,在等边三角形ABC中,点E,D分别在BC,AB上,且∠AED=60°,求证:△AEC~△EDB.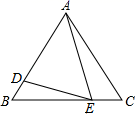 22. 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
22. 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。求证:△ADQ∽△QCP。
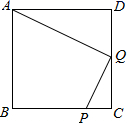 23. 如图,已知AD•AC=AB•AE , ∠DAE=∠BAC . 求证:△DAB∽△EAC .
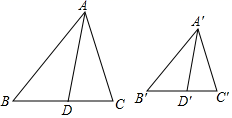
23. 如图,已知AD•AC=AB•AE , ∠DAE=∠BAC . 求证:△DAB∽△EAC .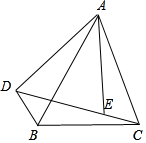 24. 如图,AD、A′D′分别是△ABC和△A′B′C′的中线,且 .判断△ABC和△A′B′C′是否相似,并说明理由.
24. 如图,AD、A′D′分别是△ABC和△A′B′C′的中线,且 .判断△ABC和△A′B′C′是否相似,并说明理由.