初中数学苏科版九年级下册6.2 黄金分割 同步训练
试卷更新日期:2021-03-04 类型:同步测试
一、单选题
-
1. 已知点P是线段AB的黄金分割点,且AP>PB,则有( )A、AB2=AP•PB B、AP2=BP•AB C、BP2=AP•AB D、AP•AB=PB•AP2. 已知如图,点 是线段 的黄金分割点( ),则下列结论中正确的是( )
 A、 B、 C、 D、3. 已知点C是线段AB的黄金分割点,且AC>BC,如果AB长为20,则AC为( )A、10 ﹣10 B、10﹣10 C、30﹣10 D、20﹣104. 生活中到处可见黄金分割的美.如图,点C将线段AB分成AC、CB两部分,且AC>BC,如果 ,那么称点C为线段AB的黄金分割点.若C是线段AB的黄金分割点,AB=2,则分割后较短线段长为( )
A、 B、 C、 D、3. 已知点C是线段AB的黄金分割点,且AC>BC,如果AB长为20,则AC为( )A、10 ﹣10 B、10﹣10 C、30﹣10 D、20﹣104. 生活中到处可见黄金分割的美.如图,点C将线段AB分成AC、CB两部分,且AC>BC,如果 ,那么称点C为线段AB的黄金分割点.若C是线段AB的黄金分割点,AB=2,则分割后较短线段长为( ) A、 B、 C、 D、5. 如图, 是线段 的黄金分割点,且 ,若 表示以 为一边的正方形的面积, 表示长为 ,宽为 的矩形的面积,则 与 的大小关系是( )
A、 B、 C、 D、5. 如图, 是线段 的黄金分割点,且 ,若 表示以 为一边的正方形的面积, 表示长为 ,宽为 的矩形的面积,则 与 的大小关系是( )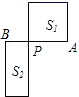 A、 B、 C、 D、无法确定6. 如图,已知点 是正方形 的边 边上的黄金分割点,且 若 表示 为边长的正方形面积, 表示以 为长, 为宽的矩形面积, 表示正方形 除去 和 剩余的面积,则 的值为( )
A、 B、 C、 D、无法确定6. 如图,已知点 是正方形 的边 边上的黄金分割点,且 若 表示 为边长的正方形面积, 表示以 为长, 为宽的矩形面积, 表示正方形 除去 和 剩余的面积,则 的值为( )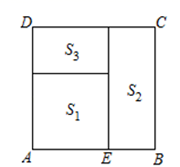 A、 B、 C、 D、7. 有以下命题:
A、 B、 C、 D、7. 有以下命题:①如果线段 是线段 , , 的第四比例项,则有 ;②如果点 是线段 的中点,那么 是 、 的比例中项;③如果点 是线段 的黄金分割点,且 ,那么 是 与 的比例中项;④如果点 是线段 的黄金分割点, ,且 ,则 .
其中正确的判断有( )
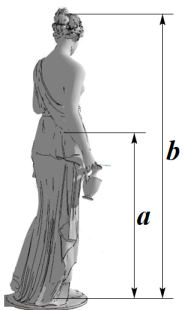
A、②④ B、①②③④ C、①③④ D、②③④8. 生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下a与全身 的高度比值接近0.618,可以增加视觉美感,若图中 为2米,则a约为( )
 A、1.24米 B、1.38米 C、1.42米 D、1.62米9. 宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称美感.我们可以用这样的方法画出黄金矩形:作正方形 ,分别取 的中点 ,连接 ,以点F为圆心,以 为半径画弧,交 的延长线于点G;作 ,交 的延长线于点H,则图中下列矩形是黄金矩形的是( )
A、1.24米 B、1.38米 C、1.42米 D、1.62米9. 宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称美感.我们可以用这样的方法画出黄金矩形:作正方形 ,分别取 的中点 ,连接 ,以点F为圆心,以 为半径画弧,交 的延长线于点G;作 ,交 的延长线于点H,则图中下列矩形是黄金矩形的是( )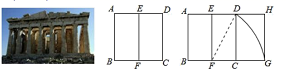 A、矩形ABEF B、矩形EFCD C、矩形EFGH D、矩形ABGH10. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )
A、矩形ABEF B、矩形EFCD C、矩形EFGH D、矩形ABGH10. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )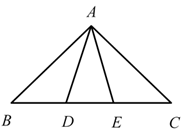 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知线段AB=6cm,点C为AB的黄金分割点,且AC>BC,则AC=.12. 已知点D是线段AB的黄金分割点,且线段AD的长为2厘米,则最短线段BD的长是厘米.13. 如图,已知点C、D是线段AB的两个黄金分割点,若线段AB的长10厘米,则线段CD长厘米.
 14. 如图,若 是已知线段,经过点 作 ,使 ;连接 ,在 上截取 ;在 上截取 ,则 .
14. 如图,若 是已知线段,经过点 作 ,使 ;连接 ,在 上截取 ;在 上截取 ,则 .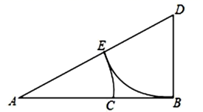 15. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么AP的长度为cm.
15. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么AP的长度为cm. 16. 古希腊时期,人们认为最美人体的肚脐至脚底的长度与身高长度之比是 ( 0.618,称之为黄金分割比例),著名的“断臂维纳斯”便是如此,若某位女性身高为165cm , 肚脐到头顶高度为65cm , 则其应穿鞋跟为cm的高跟鞋才能使人体近似满足黄金分割比例.(精确到1cm)17. 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少m处.(结果精确到0.1m)
16. 古希腊时期,人们认为最美人体的肚脐至脚底的长度与身高长度之比是 ( 0.618,称之为黄金分割比例),著名的“断臂维纳斯”便是如此,若某位女性身高为165cm , 肚脐到头顶高度为65cm , 则其应穿鞋跟为cm的高跟鞋才能使人体近似满足黄金分割比例.(精确到1cm)17. 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少m处.(结果精确到0.1m) 18. 如图,在矩形 中, , , 是 的黄金分割点( ), 是 上一点,将 沿直线 折叠,点 落在 边上的点 处,再将 沿直线 折叠,点 落在 上的点 处,则 的长为 .
18. 如图,在矩形 中, , , 是 的黄金分割点( ), 是 上一点,将 沿直线 折叠,点 落在 边上的点 处,再将 沿直线 折叠,点 落在 上的点 处,则 的长为 .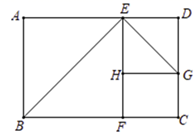
三、解答题
-
19. 已知线段AB=a,用直尺和圆规求作这条线段的黄金分割点C.
 20. 如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项.
20. 如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项. 21. 如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,求C、D之间的距离.
21. 如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,求C、D之间的距离.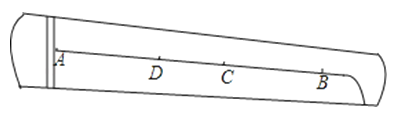 22. 人的肚脐是人的身高的黄金分割点,一般来讲,当肚脐到脚底的长度与身高的比为0.618时,是比较好看的黄金身段.一个身高1.70m的人,他的肚脐到脚底的长度为多少时才是黄金身段(保留两位小数)?23. 如果一个矩形ABCD(AB<BC)中, ≈0.618,那么这个矩形称为黄金矩形,黄金矩形给人以美感.在黄金矩形ABCD内作正方形CDEF,得到一个小矩形ABFE(如图),请问矩形ABFE是否是黄金矩形?请说明你的结论的正确性.
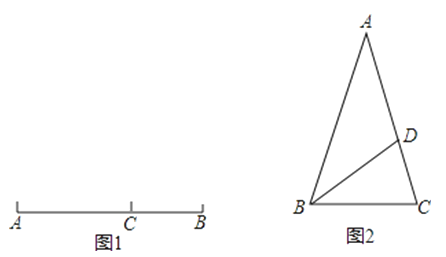
22. 人的肚脐是人的身高的黄金分割点,一般来讲,当肚脐到脚底的长度与身高的比为0.618时,是比较好看的黄金身段.一个身高1.70m的人,他的肚脐到脚底的长度为多少时才是黄金身段(保留两位小数)?23. 如果一个矩形ABCD(AB<BC)中, ≈0.618,那么这个矩形称为黄金矩形,黄金矩形给人以美感.在黄金矩形ABCD内作正方形CDEF,得到一个小矩形ABFE(如图),请问矩形ABFE是否是黄金矩形?请说明你的结论的正确性. 24. 定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
24. 定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
 25. 若矩形的一个短边与长边的比值为 ,(黄金分割数),我们把这样的矩形叫做黄金矩形
25. 若矩形的一个短边与长边的比值为 ,(黄金分割数),我们把这样的矩形叫做黄金矩形 (1)、操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD.(2)、探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由.(3)、归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)26. 如图①,我们已经学过:点C将线段AB分成两部分(AC>BC),如果 ,那么称点C为线段AB的黄金分割点,某班在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1 , S2(S1>S2),如果 ,那么称直线l为该图形的黄金分割线,如图②,在△ABC中,∠A=36º,AB=AC,∠ACB的平分线交AB于点D
(1)、操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD.(2)、探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由.(3)、归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)26. 如图①,我们已经学过:点C将线段AB分成两部分(AC>BC),如果 ,那么称点C为线段AB的黄金分割点,某班在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1 , S2(S1>S2),如果 ,那么称直线l为该图形的黄金分割线,如图②,在△ABC中,∠A=36º,AB=AC,∠ACB的平分线交AB于点D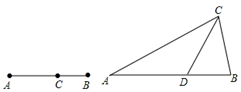 (1)、求证:点D是AB边上的黄金分割点;(2)、求证:直线CD是△ABC的黄金分割点27. 定义:如图1,点P为线段AB上一点,如果 =k,那么我们称点P是线段AB的黄金分割点, 叫做黄金分割数.
(1)、求证:点D是AB边上的黄金分割点;(2)、求证:直线CD是△ABC的黄金分割点27. 定义:如图1,点P为线段AB上一点,如果 =k,那么我们称点P是线段AB的黄金分割点, 叫做黄金分割数.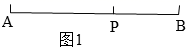
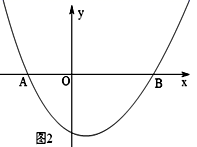 (1)、理解:利用图1,运用一元二次方程的知识,求证:黄金分割数 ;(2)、应用:如图2,抛物线y=x2+nx+2n(n<0)的图象与x轴交于A、B两点(OA<OB),若原点O是线段AB的黄金分割点,①求线段AB的长;②直接写出点A和点B的坐标.
(1)、理解:利用图1,运用一元二次方程的知识,求证:黄金分割数 ;(2)、应用:如图2,抛物线y=x2+nx+2n(n<0)的图象与x轴交于A、B两点(OA<OB),若原点O是线段AB的黄金分割点,①求线段AB的长;②直接写出点A和点B的坐标.