广西壮族自治区贺州市2021届九年级上学期数学12月月考试卷
试卷更新日期:2021-03-04 类型:月考试卷
一、单选题
-
1. 抛物线 的对称轴是( )A、直线 B、直线 C、直线 D、直线2. 如图,在 中, ,设 、 , 所对的边分别为a,b,c,则下列等式成立的是( )
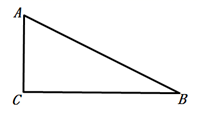 A、 B、 C、 D、3. 把抛物线 平移得到抛物线 ,是怎样平移得到的( )A、向右平移7个单位长度、再向下平移3个单位长度 B、向左平移3个单位长度,再向上平移7个单位长度 C、向右平移3个单位长度,再向上平移7个单位长度 D、向左平移3个单位长度,再向下平移7个单位长度4. 如图,直线 ,直线 分别交 , , 于点 , , ;直线 分别交 , , 于点 , , , 与 相交于点 ,且 , , ,则 的值为( )
A、 B、 C、 D、3. 把抛物线 平移得到抛物线 ,是怎样平移得到的( )A、向右平移7个单位长度、再向下平移3个单位长度 B、向左平移3个单位长度,再向上平移7个单位长度 C、向右平移3个单位长度,再向上平移7个单位长度 D、向左平移3个单位长度,再向下平移7个单位长度4. 如图,直线 ,直线 分别交 , , 于点 , , ;直线 分别交 , , 于点 , , , 与 相交于点 ,且 , , ,则 的值为( )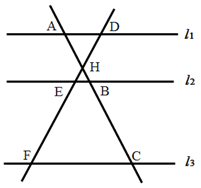 A、 B、 C、 D、5. 对于函数 ,下列说法错误的是( )A、点 在这个函数图象上 B、这个函数的图象位于第一、三象限 C、函数的图象是轴对称图形 D、y随x的增大而减小6. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A、 B、 C、 D、5. 对于函数 ,下列说法错误的是( )A、点 在这个函数图象上 B、这个函数的图象位于第一、三象限 C、函数的图象是轴对称图形 D、y随x的增大而减小6. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )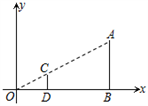 A、(2,1) B、(2,0) C、(3,3) D、(3,1)7. 已知二次函数 的图象如图所示,则下列结论正确的是( )
A、(2,1) B、(2,0) C、(3,3) D、(3,1)7. 已知二次函数 的图象如图所示,则下列结论正确的是( )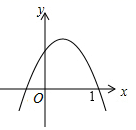 A、 B、 C、 D、8. 如图,在 中, , ,垂足为D, , ,则CB的长为( )
A、 B、 C、 D、8. 如图,在 中, , ,垂足为D, , ,则CB的长为( ) A、 B、4 C、12 D、169. 反比例函数y= (k≠0)与二次函数y=x2+kx-k的大致图象是( )A、
A、 B、4 C、12 D、169. 反比例函数y= (k≠0)与二次函数y=x2+kx-k的大致图象是( )A、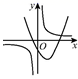 B、
B、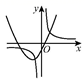 C、
C、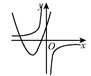 D、
D、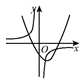 10. 下列命题:①两个相似多边形面积之比等于相似比的平方:②两个相似三角形的对应高之比等于它们的相似比;③在 与 中, , ,那么 ;④已知 及位似中心O,能够作一个且只能作一个三角形与 位似,使位似比为2其中真命题的个数是( )A、1个 B、2个 C、3个 D、4个11. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( )
10. 下列命题:①两个相似多边形面积之比等于相似比的平方:②两个相似三角形的对应高之比等于它们的相似比;③在 与 中, , ,那么 ;④已知 及位似中心O,能够作一个且只能作一个三角形与 位似,使位似比为2其中真命题的个数是( )A、1个 B、2个 C、3个 D、4个11. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ) A、
A、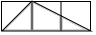 B、
B、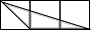 C、
C、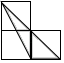 D、
D、 12. 如图,E是矩形ABCD的边CD上的点,BE交AC于O,已知 与 的面积分别为2和8,则四边形AOED的面积为( )
12. 如图,E是矩形ABCD的边CD上的点,BE交AC于O,已知 与 的面积分别为2和8,则四边形AOED的面积为( )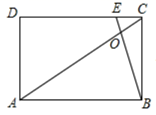 A、16 B、32 C、38 D、40
A、16 B、32 C、38 D、40二、填空题
-
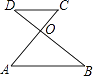
13. 如图,线段AC、BD交于点O,请你添加一个条件: , 使△AOB∽△COD.
 14. 已知在 中, , ,那么 的值等于.15. 如图,在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需米.
14. 已知在 中, , ,那么 的值等于.15. 如图,在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需米.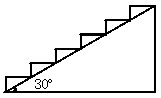 16. 如图,在 中, , ,D为BC边上的一点,且 .若 的面积为1,则 的面积为.
16. 如图,在 中, , ,D为BC边上的一点,且 .若 的面积为1,则 的面积为.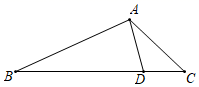 17. 某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x﹣1.5x2 , 该型号飞机着陆后滑行m才能停下来.18. 已知二次函数 的图象如图所示,下列4个结论:① ;② ;③ ;④ .其中正确的结论有.
17. 某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x﹣1.5x2 , 该型号飞机着陆后滑行m才能停下来.18. 已知二次函数 的图象如图所示,下列4个结论:① ;② ;③ ;④ .其中正确的结论有.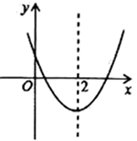
三、解答题
-
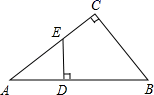
19. 计算: .20. 如图,在△ABC中,∠C=90°,在AB边上取一点D,使BD=BC,过D作DE⊥AB交AC于E,AC=8,BC=6,求DE的长.
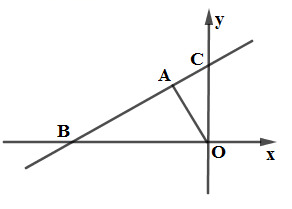
 21. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于A、B两点,已知 , .
21. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于A、B两点,已知 , .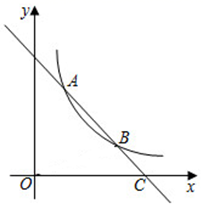 (1)、求反比例函数的表达式;(2)、当 时,求不等式 的解集.22. 2020年春节期间,新型冠状病毒肆虐,突如其来的疫情让大多数人不能外出,网络销售成为这个时期最重要的一种销售方式.某镇贸易公司因此开设了一家网店,销售当地某种农产品.已知该农产品成本为每千克10元.调查发现,每天销售量y(kg)与销售单价x(元)满足函数关系 (其中 ).(1)、当销售单价为12元时,每天的销售利润为元:当销售单价为20元时,每天的销售利润为元.(2)、当销售单价为多少元时,每天的销售利润最大?最大利润是多少元?23. 九年级数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为20米的发射塔AB,如图所示.在山脚平地上的D处测得塔底B的仰角为 ,向小山前进100米到达点E处,测得塔顶A的仰角为 ,求小山BC的高度.(结果保留根号)
(1)、求反比例函数的表达式;(2)、当 时,求不等式 的解集.22. 2020年春节期间,新型冠状病毒肆虐,突如其来的疫情让大多数人不能外出,网络销售成为这个时期最重要的一种销售方式.某镇贸易公司因此开设了一家网店,销售当地某种农产品.已知该农产品成本为每千克10元.调查发现,每天销售量y(kg)与销售单价x(元)满足函数关系 (其中 ).(1)、当销售单价为12元时,每天的销售利润为元:当销售单价为20元时,每天的销售利润为元.(2)、当销售单价为多少元时,每天的销售利润最大?最大利润是多少元?23. 九年级数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为20米的发射塔AB,如图所示.在山脚平地上的D处测得塔底B的仰角为 ,向小山前进100米到达点E处,测得塔顶A的仰角为 ,求小山BC的高度.(结果保留根号)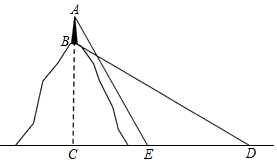 24. 如图,在平行四边形ABCD中,M为对角线AC上一点,BM的延长线交AD于点N,交CD的延长线于点E.
24. 如图,在平行四边形ABCD中,M为对角线AC上一点,BM的延长线交AD于点N,交CD的延长线于点E.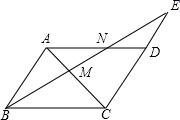 (1)、请找出一对相似的三角形并证明;(2)、若 , ,求BE的长.
(1)、请找出一对相似的三角形并证明;(2)、若 , ,求BE的长.