浙江金华义乌廿三里大陈等校联考2020-2021学年八年级上学期第三次月考数学试题
试卷更新日期:2021-03-04 类型:月考试卷
一、单选题
-
1. 下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各点中,在第二象限的点是( )A、 B、 C、 D、3. 满足下列条件的△ABC不是直角三角形的是( )A、BC=1,AC=2,AB= B、BC:AC:AB=3:4:5 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:54. 不等式组 的解集在数轴上表示正确的是( )A、
2. 下列各点中,在第二象限的点是( )A、 B、 C、 D、3. 满足下列条件的△ABC不是直角三角形的是( )A、BC=1,AC=2,AB= B、BC:AC:AB=3:4:5 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:54. 不等式组 的解集在数轴上表示正确的是( )A、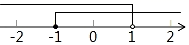 B、
B、 C、
C、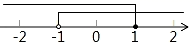 D、
D、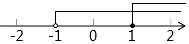 5. 能说明命题“对于任何实数 ”是假命题的一个反例可以是( )A、 B、 C、 D、6. 如图,在△ABC中,BF、CF分别平分∠ABC和∠ACB , 过点F作EG∥BC分别交于点AB、AC于点E、G . 若AB=9,BC=10,AC=11,则△AEG的周长为( )
5. 能说明命题“对于任何实数 ”是假命题的一个反例可以是( )A、 B、 C、 D、6. 如图,在△ABC中,BF、CF分别平分∠ABC和∠ACB , 过点F作EG∥BC分别交于点AB、AC于点E、G . 若AB=9,BC=10,AC=11,则△AEG的周长为( )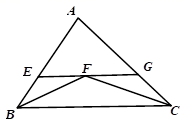 A、15 B、20 C、21 D、197. 若关于x的不等式 只有2个正整数解,则a的取值范围为( )A、 B、 C、 D、8. 已知:将直线 向左平移2个单位长度后得到直线 ,则下列关于直线 的说法正确的是( )A、经过第一、二、三象限 B、与x轴交于 C、与y轴交于 D、y随x的增大而减小9. 某水电站蓄水池有2个进水口,1个出水口,每个进水口进水量 与时间x的关系为 ,出水口出水量 与时间x的关系为 ,已知某天0点到6点,进行机组试运行,试机时至少打开1个水口,且水池的蓄水量V与时间的关系.如图所示:给出以下判断:①0到3点只进水不出水;②3点到4点,不进水只出水;③4点到6点不进水也不出水.则上述判断中一定正确的是( )
A、15 B、20 C、21 D、197. 若关于x的不等式 只有2个正整数解,则a的取值范围为( )A、 B、 C、 D、8. 已知:将直线 向左平移2个单位长度后得到直线 ,则下列关于直线 的说法正确的是( )A、经过第一、二、三象限 B、与x轴交于 C、与y轴交于 D、y随x的增大而减小9. 某水电站蓄水池有2个进水口,1个出水口,每个进水口进水量 与时间x的关系为 ,出水口出水量 与时间x的关系为 ,已知某天0点到6点,进行机组试运行,试机时至少打开1个水口,且水池的蓄水量V与时间的关系.如图所示:给出以下判断:①0到3点只进水不出水;②3点到4点,不进水只出水;③4点到6点不进水也不出水.则上述判断中一定正确的是( ) A、① B、② C、②③ D、①③
A、① B、② C、②③ D、①③二、填空题
-
10. 函数 中,自变量x的取值范围是 .11. 等腰三角形的周长为20 cm,一边长为8 cm,则底边长为cm.12. 如图,在正方形网格中有两个小正方形被涂黑,再涂黑一个图中其余的小正方形,使得整个被涂黑的图案构成一个轴对称图形,那么涂法共有种.
 13. 将长方形纸片ABCD沿对角线BD折叠,点C落在点 处, 交AD于点E.若 ,对角线 ,则 .
13. 将长方形纸片ABCD沿对角线BD折叠,点C落在点 处, 交AD于点E.若 ,对角线 ,则 . 14. 如图所示,在 中, ,以BC为斜边向外侧做等腰直角 ,过点D做 于点E,若线段 , ,则 .
14. 如图所示,在 中, ,以BC为斜边向外侧做等腰直角 ,过点D做 于点E,若线段 , ,则 . 15. 定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若 , ,则P,Q的“实际距离”为5,即 或 .环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为 , , ,若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为.
15. 定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若 , ,则P,Q的“实际距离”为5,即 或 .环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为 , , ,若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为.
三、解答题
-
16. 解下列不等式(组)(1)、 ;(2)、 .17. 如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点, 的三个顶点均在格点上.

( 1 )将 先向右平移6个单位长度,再向上平移3个单位长度,得到 ,画出平移后的 ;
( 2 )建立适当的平面直角坐标系,使得点 的坐为 ;
( 3 )在(2)的条件下,直接写出点 的坐标.
18. 已知:如图∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD. 19. 如图,直线 与过点 的直线 交于点 ,与x轴交于点B.
19. 如图,直线 与过点 的直线 交于点 ,与x轴交于点B. (1)、求直线 的解析式;(2)、求 的面积;(3)、直接写出当自变量x取何值时,满足 ?20. 某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件40元,乙种奖品每件30元(1)、如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件?(2)、如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案?21. 已知点A(8,0)及在第一象限的动点B(x,y),且x+y=10,设 OBA的面积为S.
(1)、求直线 的解析式;(2)、求 的面积;(3)、直接写出当自变量x取何值时,满足 ?20. 某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件40元,乙种奖品每件30元(1)、如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件?(2)、如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案?21. 已知点A(8,0)及在第一象限的动点B(x,y),且x+y=10,设 OBA的面积为S.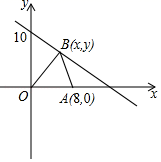 (1)、求S关于x的函数关系式,并写出自变量x的取值范围;(2)、求S=12时B点坐标;(3)、在(2)的基础上,设点Q为y轴上一动点,当BQ+AQ的值最小时,求Q点坐标.22. 如图,边长为2的正方形ABCD中,P是对角线AC上的一个动点(点P不与A、C重合),连结BP,过点B作 且使得 ,连结QP交BC于点E,延长QP与直线AD交于点F.
(1)、求S关于x的函数关系式,并写出自变量x的取值范围;(2)、求S=12时B点坐标;(3)、在(2)的基础上,设点Q为y轴上一动点,当BQ+AQ的值最小时,求Q点坐标.22. 如图,边长为2的正方形ABCD中,P是对角线AC上的一个动点(点P不与A、C重合),连结BP,过点B作 且使得 ,连结QP交BC于点E,延长QP与直线AD交于点F. (1)、 面积的最小值为;(2)、连结CQ,求证: ;(3)、猜想PF与EQ的数量关系,并说明理由.23. 定义:在平面直角坐标系中,对于任意两点 , ,若点 满足 , ,那么称点 是点 , 的融合点.
(1)、 面积的最小值为;(2)、连结CQ,求证: ;(3)、猜想PF与EQ的数量关系,并说明理由.23. 定义:在平面直角坐标系中,对于任意两点 , ,若点 满足 , ,那么称点 是点 , 的融合点.例如: , ,当点 满是 , 时,则点 是点 , 的融合点,
 (1)、已知点 , , ,请说明其中一个点是另外两个点的融合点.(2)、如图,点 ,点 是直线 上任意一点,点 是点 , 的融合点.
(1)、已知点 , , ,请说明其中一个点是另外两个点的融合点.(2)、如图,点 ,点 是直线 上任意一点,点 是点 , 的融合点.①试确定 与 的关系式.
②若直线 交 轴于点 ,当 为直角三角形时,求点 的坐标.