河南省林州市2020-2021学年八年级上学期数学第三次月考试卷(B卷)
试卷更新日期:2021-03-04 类型:月考试卷
一、单选题
-
1. 等腰三角形的两边长分别为4cm和8cm,则它的周长为( )A、16cm B、17cm C、20cm D、16cm或20cm2. 已知,点 与点 关于 轴对称,则 的值为( )A、 B、1 C、-1 D、3. 下列各式: , , , , 其中分式有( )A、1个 B、2个 C、3个 D、4个4. 若单项式 和 的积为 ,则 的值为( )A、2 B、30 C、-15 D、155. 若 , ,则 的值为( )A、 B、-2 C、 D、6. 下列四个多项式:①-a2+b2;②-x2-y2;③1-(a-1)2;④x2-2xy+y2 , 其中能用平方差公式分解因式的有( )A、4个 B、3个 C、2个 D、1个7. 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( )
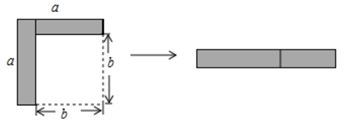 A、 B、 C、 D、8. 如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=( )
A、 B、 C、 D、8. 如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=( ) A、10° B、15° C、20° D、30°9. 如图,是由大小一样的小正方形组成的网格,△ABC的三个顶点均落在小正方形的顶点上.在网格上能画出的三个顶点都落在小正方形的顶点上,且与△ABC成轴对称的三角形共有( )
A、10° B、15° C、20° D、30°9. 如图,是由大小一样的小正方形组成的网格,△ABC的三个顶点均落在小正方形的顶点上.在网格上能画出的三个顶点都落在小正方形的顶点上,且与△ABC成轴对称的三角形共有( )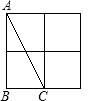 A、5个 B、4个 C、3个 D、2个10. 如图,已知△ ABC中,AB=AC,∠BAC=90°,直角∠ EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形; ③2S四边形AEPF=S△ ABC; ④BE+CF=EF.当∠ EPF在△ABC内绕顶点P旋转时(点E与A,B重合).上述结论中始终正确的有( )
A、5个 B、4个 C、3个 D、2个10. 如图,已知△ ABC中,AB=AC,∠BAC=90°,直角∠ EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形; ③2S四边形AEPF=S△ ABC; ④BE+CF=EF.当∠ EPF在△ABC内绕顶点P旋转时(点E与A,B重合).上述结论中始终正确的有( )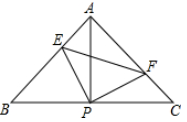 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
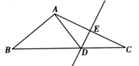
11. 如图, 中, 是 的垂直平分线, , 的周长为16 ,则 的周长为.
 12. 计算 等于.13. 如果 是一个完全平方式,那么m的值 .14. 已知 与 的积中不 项和 项,则 =15. 如图所示,两个正方形的边长分别为a和b,如果a+b=10,ab=20,那么阴影部分的面积是.
12. 计算 等于.13. 如果 是一个完全平方式,那么m的值 .14. 已知 与 的积中不 项和 项,则 =15. 如图所示,两个正方形的边长分别为a和b,如果a+b=10,ab=20,那么阴影部分的面积是.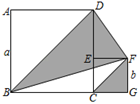
三、解答题
-
16. 先化简,再求值:(2+3x)(2﹣3x)+5x(x﹣1)+(2x﹣1)2 , 其 .17. 分解因式.(1)、9m²-4;(2)、2ax²+12ax+18a;(3)、(x+3)(x-5)+ x²-9.18. 甲乙两人共同计算一道整式乘法: ,甲把第二个多项式中 前面的减号抄成了加号,得到的结果为 ,乙漏抄了第二个多项式中 的系数 ,得到的结果为 .(1)、计算出 、 的值;(2)、求出这道整式乘法的正确结果.19. 如图, 的三个顶点在边长为1的正方形网格中,已知 , , .
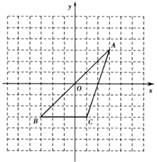 (1)、画出 关于y轴对称的 ,且点A的对应点为 ,点B的对应点为 ,点C的对应点为 ;(2)、在(1)的条件下, , , 的坐标分别是 , , ;(3)、请直接写出第四象限内以 为边且与 全等的三角形的第三个顶点(不与C重合)的坐标,这点的坐标为.20. 如图,点D是 边 上一点, ,过B点作 ,且 ,连接 交 于点O,连接 .求证: 平分 .
(1)、画出 关于y轴对称的 ,且点A的对应点为 ,点B的对应点为 ,点C的对应点为 ;(2)、在(1)的条件下, , , 的坐标分别是 , , ;(3)、请直接写出第四象限内以 为边且与 全等的三角形的第三个顶点(不与C重合)的坐标,这点的坐标为.20. 如图,点D是 边 上一点, ,过B点作 ,且 ,连接 交 于点O,连接 .求证: 平分 .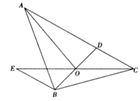 21. 如图在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于点F,交AB于点E.求证:BF= FC.
21. 如图在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于点F,交AB于点E.求证:BF= FC.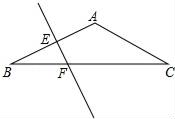 22. 如图, 中, , .
22. 如图, 中, , .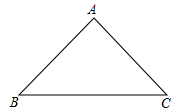 (1)、请用尺规作图的方法在边 上确定点 ,使得 平分 ;(保留作图痕迹,不写作法)(2)、在(1)的条件下,求证: .23. 在平面直角坐标系中,点 , ,点C为x轴正半轴上一动点,过点A作 交y轴于点E.
(1)、请用尺规作图的方法在边 上确定点 ,使得 平分 ;(保留作图痕迹,不写作法)(2)、在(1)的条件下,求证: .23. 在平面直角坐标系中,点 , ,点C为x轴正半轴上一动点,过点A作 交y轴于点E.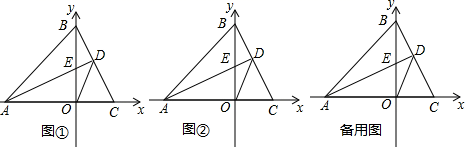 (1)、如图 ,若点C的坐标为 ,试求点E的坐标;(2)、如图 ,若点C在x轴正半轴上运动,且 , 其它条件不变,连接DO,求证:OD平分(3)、若点C在x轴正半轴上运动,当 时,求 的度数.24. 如图, 是边长为3的等边三角形, 是 边上的一个动点,由 向 运动( 不与 重合), 是 延长线上一动点,与点 同时以相同的速度由 向 延长线方向运动( 不与 重合)
(1)、如图 ,若点C的坐标为 ,试求点E的坐标;(2)、如图 ,若点C在x轴正半轴上运动,且 , 其它条件不变,连接DO,求证:OD平分(3)、若点C在x轴正半轴上运动,当 时,求 的度数.24. 如图, 是边长为3的等边三角形, 是 边上的一个动点,由 向 运动( 不与 重合), 是 延长线上一动点,与点 同时以相同的速度由 向 延长线方向运动( 不与 重合)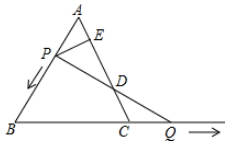 (1)、当 时,求 的长.(2)、过 作 于点 ,连结 交 于 ,在点 的运动过程中,线段 的长是否发生变化?若不变,求出 的长度;若变化,求出变化范围.
(1)、当 时,求 的长.(2)、过 作 于点 ,连结 交 于 ,在点 的运动过程中,线段 的长是否发生变化?若不变,求出 的长度;若变化,求出变化范围.