浙江省绍兴市柯桥区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-04 类型:期末考试
一、选择题(每小题2分,共20分)
-
1. −4的绝对值是( )A、-4 B、- C、4 D、2. 国务院总理李克强2020年5月22日在作政府工作报告时说,去年我国农村贫困人口减少11090000,脱贫攻坚取得决定性成就,数据11090000用科学记数法表示为( )A、1109×104 B、11.09×106 C、1.109×108 D、1.109×1073. 如图所示,能用∠O,∠AOB,∠1三种方法表示同一个角的图形是( )A、
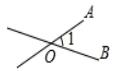 B、
B、 C、
C、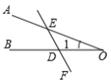 D、
D、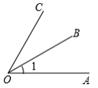 4. , , , , 中无理数的个数为( )A、4个 B、3个 C、2个 D、1个5. 二元一次方程2 x-y =1有无数多个解,下列四组值中是该方程的解的是( )A、 B、 C、 D、6. 如果单项式 与 是同类项,那么 的值分别是( )A、3,2 B、2,2 C、3,4 D、2,47. 将一元一次方程 去分母后,得( )A、2x - x - 2 = 4 B、2x - x + 2 = 1 C、2x - (x - 2) = 4 D、2x - (x - 2) = 18. 在直线AB上任取一点O,过点O作射线OC、OD,使∠COD=100°,当∠AOC=30° 时,∠BOD的度数是( )A、50° B、80° C、80°或150° D、50°或110°9. 为解决村庄灌溉问题,政府投资由水库向A,B,C,D,E这五个村庄铺设管道,现已知这五个村庄与水库以及村与村之间的距离(单位:km)如图所示,则把水库的水输送到这五个村庄铺设管道的总长度最短应是( )
4. , , , , 中无理数的个数为( )A、4个 B、3个 C、2个 D、1个5. 二元一次方程2 x-y =1有无数多个解,下列四组值中是该方程的解的是( )A、 B、 C、 D、6. 如果单项式 与 是同类项,那么 的值分别是( )A、3,2 B、2,2 C、3,4 D、2,47. 将一元一次方程 去分母后,得( )A、2x - x - 2 = 4 B、2x - x + 2 = 1 C、2x - (x - 2) = 4 D、2x - (x - 2) = 18. 在直线AB上任取一点O,过点O作射线OC、OD,使∠COD=100°,当∠AOC=30° 时,∠BOD的度数是( )A、50° B、80° C、80°或150° D、50°或110°9. 为解决村庄灌溉问题,政府投资由水库向A,B,C,D,E这五个村庄铺设管道,现已知这五个村庄与水库以及村与村之间的距离(单位:km)如图所示,则把水库的水输送到这五个村庄铺设管道的总长度最短应是( )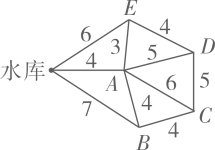 A、19km B、20km C、21 km D、22 km10. 自行车的轮胎安装在前轮上行驶3000千米后报废,安装在后轮上,只能行驶2000千米,为了行驶尽可能多的路程,采取在自行车行驶一定路程后,用前后轮调换使用的方法,那么安装在自行车上的这对轮胎最多可行驶多少千米?( )A、2300千米 B、2400千米 C、2500千米 D、2600千米
A、19km B、20km C、21 km D、22 km10. 自行车的轮胎安装在前轮上行驶3000千米后报废,安装在后轮上,只能行驶2000千米,为了行驶尽可能多的路程,采取在自行车行驶一定路程后,用前后轮调换使用的方法,那么安装在自行车上的这对轮胎最多可行驶多少千米?( )A、2300千米 B、2400千米 C、2500千米 D、2600千米二、填空题(每小题3分,共30分)
-
11. -2的相反数为;9的算术平方根为;4的倒数为.12. 3.(选填“>”、“<”或“=”)13. 已知x=2是方程6x-mx+4=0的解,那么m的值为.14. 将0.09493用四舍五入法取近似值精确到百分位,其结果是.15. 已知|x+y-5]+(x-y+3)2=0,则xy=.16. 如果代数式a2+2a的值为5,那么代数式2a2+4a-3的值为.17. 已知一个角的余角比这个角的补角的一半小25°,那么这个角的度数为.18. 已知|a|=3 ,|b|=2,且|a-bl=b-a,则a+b=.19. 如图,C、D是线段AB上两点,已知图中所有线段的长度都是正整数,且总和为35,则线段AB的长度为.
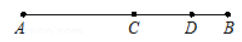 20. 将正奇数按如图所示的规律排列:
20. 将正奇数按如图所示的规律排列:
则2021在第行,从左向右第个数.
三、解答题(本大题共有8小题,共50分)
-
21. 计算:(1)、3-(-8)+(-5)+6;(2)、22. 解方程(组):(1)、(2)、23. 如图,已知线段DA与B、C两点,用圆规和无刻度的直尺按下列要求画图并计算:
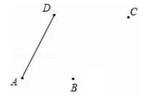 (1)、①画直线AB、射线DC;
(1)、①画直线AB、射线DC;
②延长线段DA至点E,使AE=AB(保留作图痕迹);(2)、若AB=2cm,AD=4cm,求线段DE的长.24. 先化简,再求值:,其中a=﹣1,b=﹣2
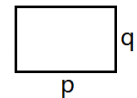
25. 已知,如图直线AB与CD相交于点O,∠BOE=90°,∠AOD=30°,OF为∠BOD的角平分线.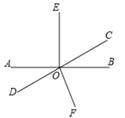 (1)、求∠EOC度数;(2)、求∠EOF的度数.26. 关于x、y的二元一次方程组 与 的解相同,求a、b的值.27. 阅读下列材料:如图,长方形的周长为2(p+q),面积为pq,等式2(p+q)=pq在一般情形下不成立,但有些特殊数可以使它成立,例如: p=4,q=4时,
(1)、求∠EOC度数;(2)、求∠EOF的度数.26. 关于x、y的二元一次方程组 与 的解相同,求a、b的值.27. 阅读下列材料:如图,长方形的周长为2(p+q),面积为pq,等式2(p+q)=pq在一般情形下不成立,但有些特殊数可以使它成立,例如: p=4,q=4时,2(4+4)=4x4成立,我们称(4,4)为2(p+q) =pq成立的“和谐数对”.
请完成下列问题:
 (1)、若(3,x)是2(p+q)=pq成立的“和谐数对”,则x=;(2)、写出一对2(p+q)=pq成立的“和谐数对”(p,q),其中p≠3,p≠4;(3)、若(m,n)是2(p+tq)=pq成立的“和谐数对”,
(1)、若(3,x)是2(p+q)=pq成立的“和谐数对”,则x=;(2)、写出一对2(p+q)=pq成立的“和谐数对”(p,q),其中p≠3,p≠4;(3)、若(m,n)是2(p+tq)=pq成立的“和谐数对”,求代数式-(4m+12n)-[2m-2(3n+ mn+ )]的值.
28. 如图1,现有一个棱长为20cm的立方体水槽放在桌面上,水槽内水的高度为acm,往水槽里放入棱长为10cm的立方体铁块. (1)、求下列两种情况下a的值.
(1)、求下列两种情况下a的值.①若放入铁块后水面恰好在铁块的上表面,则a=cm;②若放入铁块后水槽恰好盛满(无溢出),则a=cm;
(2)、若0≤a≤7.5,放入铁块后水槽内水面的高度为cm,(用含a的代数式表示).(3)、如图2,在水槽旁用管子连通一个底面在桌面上的圆柱形容器,内部底面积为50cm2 , 管口底部A离水槽内底面的高度为hcm (h>a),水槽内放入铁块,水溢入圆柱形容器后,容器内水面与水槽内水面的高度差为4cm,若 a=15,求h的值.(水槽和容器的壁及底面厚度相同)