浙江省宁波市慈溪市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-04 类型：期末考试

进入出卷网下载

一、选择题（每题4分，共40分）

1. 下列各图中，能通过一个三角形绕一点旋转一次得到另一三角形的图形是（）

A、 B、 C、 D、

查看试题解析
2. 气象台预报明天下雨的概率为70%，则下列理解正确的是（）

A、明天30%的地区不会下雨 B、明天下雨的可能性较大 C、明天70%的时间会下雨 D、明天下雨是必然事件

查看试题解析
3. 把二次函数 $y = {(x - 1)}^{2} - 3$ 的图象向左平移3个单位，向上平移4个单位后，得到的图象所对应的二次函数表达式为（）

A、 $y = {(x + 2)}^{2} + 1$ B、 $y = {(x - 2)}^{2} + 1$ C、 $y = {(x + 4)}^{2} + 1$ D、 $y = {(x - 4)}^{2} + 1$

查看试题解析
4. 一个圆的内接正六边形与内接正方形的边长之比为（）

A、3：2 B、 $1 ： \sqrt{3}$ C、 $1 ： \sqrt{2}$ D、 $\sqrt{2} ： \sqrt{3}$

查看试题解析
5. 如图，直线l₁∥l₂∥l₃ ，直线AB，DE分别交l₁ ， l₂ ， l₃于点A，B，C和D，E，F，若AB：AC=2：5，EF=15，则DF的长等于（）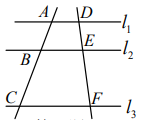

A、18 B、20 C、25 D、30

查看试题解析
6. 在4×5网格中，A，B，C为如图所示的格点（小正方形的顶点），则下列等式正确的是（）

A、sinA= $\frac{\sqrt{3}}{2}$ B、cosA= $\frac{1}{2}$ C、tanA= $\frac{\sqrt{3}}{3}$ D、cosA= $\frac{\sqrt{2}}{2}$

查看试题解析
7. 如图，已知⊙O的半径为3，弦AB⊥直径CD，∠A＝30°，则 $\overset{⏜}{B D}$ 的长为（）

A、π B、2π C、3π D、6π

查看试题解析
8. 如图，某商场为了便于残疾人的轮椅行走，准备拆除台阶换成斜坡，又考虑安全，斜坡的坡角不得超过10°，此商场门前的台阶高出地面1.53米，则斜坡的水平宽度AB至少需（）（精确到0.1米．参考值：sin10°≈17，cos10°≈98，tan10°≈18)

A、8.5米 B、8.8米 C、8.3米 D、9米

查看试题解析
9. 如图，矩形相框的外框矩形的长为12dm，宽为8dm，上下边框的宽度都为xdm，左右边框的宽度都为ydm．则符合下列条件的x，y的值能使内边框矩形和外边框矩形相似的为（）

A、x=y B、3x=2y C、x=1，y=2 D、x=3，y=2

查看试题解析
10. 如图，二次函数 $y = a x^{2} + b x + c$ （a≠0，a，b，c为常数）与二次函数 $y = \frac{1}{2} x^{2} + e x + f$ （e，f为常数）的图象的顶点分别为A，B，且相交于C（m，n）和D（m+8，n）.若∠ACB=90°，则a的值为（）

A、 $- \frac{1}{2}$ B、 $- \frac{1}{4}$ C、 $- \frac{1}{8}$ D、 $- \frac{1}{16}$

查看试题解析

二、填空题（每题5分，共30分）

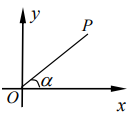
11. 如图，已知P（4，3）为∠ $α$ 边上一点，则cos $α$ = ．

查看试题解析

12. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球, 某学习小组做摸球实验, 将球搅匀后从中随机摸出一个球记下颜色, 再把它放回袋中, 不断重复. 下表是活动进行中的一组统计数据：

摸球的次数n	100	150	200	500	800	1000	6000
摸到白球的次数m	58	96	116	295	484	601	3601
摸到白球的频率 $\frac{m}{n}$	0.58	0.64	0.58	0.59	0.605	0.601	0.600

小杰根据表格中的数据提出了下列两个判断:①若摸10000次，则频率一定为0.6;②可以估计摸一次得白球的概率约为0.6.则这两个判断正确的是(若有正确的，则填编号﹔若没有正确的，则填“无”).

查看试题解析

13. 已知，点A ( -1，y₁ )，B (-0.5，y₂)，C(4，y₃)都在二次函数y=—ax²+2ax-1(a>0）的图象上，则y₁ ， y₂ ， y₃的大小关系是

查看试题解析
14. 如图，AB为OO的直径， $\overset{⌢}{A C} = 2 \overset{⌢}{B C}$ ，M为 $\overset{⌢}{B C}$ 的中点，过M作MNllOC交AB于N，连结BM，则∠BMN的度数为

查看试题解析
15. 如图，将一张面积为10的大三角形纸片沿着虚线剪成三张小三角形纸片与一张平行四边形纸片．根据图中标示的长度，则平行四边形纸片的面积为．

查看试题解析
16. 如图1是2002年发行的中国纪念邮票，其图案是三国时期吴国数学家赵爽在注释《周髀算经》中所给勾股定理的证明．同学们在探索勾股定理时还出现了许多利用正方形证明勾股定理的方法．如图2，正方形ABCD是由四个全等的直角三角形和一个正方形EFGH拼成；正方形EFGH是由与上述四个直角三角形全等的三角形和正方形IJKL拼成；正方形ABCD，EFGH，IJKL的面积分别为S₁ ， S₁ ， S₃分别连结AK，BL，CI，DJ并延长构成四边形MNOP，它的面积为m．①请用等式表示S₁ ， S₁ ， S₃之间的数量关系为：；②m=（用含S₁ ， S₃的代数式表示m）

查看试题解析

三、解答题（第17、18、19题各8分，第20、21、22题各10分，第23题12分，第24题14分，共80分）

17. 计算求值：

(1)、已知 $\frac{a}{b} = \frac{3}{4}$ ，求 $\frac{a - b}{a}$ 的值.

(2)、2sin30°-tan60°×cos30°

查看试题解析
18. 如图，在4×8的网格中，已知格点△ABC（小正方形的顶点称为格点，顶点在格点处的三角形称为格点三角形），在图1、图2中分别画一个格点三角形（所画的两个三角形不全等），使其同时符合下列两个条件.

（ 1 ）与△ABC有一公共角；

（ 2 ）与△ABC相似但不全等.

查看试题解析
19. 某校在防疫期间开设A，B，C三个测体温通道.一天早晨，小丽与小聪任意选择一个通道进入校园.

(1)、求小丽通过A通道进入校园的概率；

(2)、利用画树状图或列表的方法，求小丽和小聪从两个不同通道进入校园的概率（要求画出树状图或表格）.

查看试题解析
20. 有一种落地晾衣架如图1所示，其原理是通过改变两根支撑杆夹角α的度数来调整晾衣杆的高度，图2是晾衣架的侧面的平面示意图，AB和CD分别是两根长度不等的支撑杆，夹角∠BOD=α，AO=70cm，BO=DO=80cm，CO=40cm.

(1)、若α=56°，求A点离地面的高度AE.
(参考值： sin62°=cos28≈0.88 ， sin 28°=cos62°≈0.47，tan62°≈1.88，tan 28°≈0.53.)

(2)、调节α的大小，使A离地面高度AE=125 cm时，求此时C点离地面的高度CF.

查看试题解析
21. 如图，用长为24米的篱笆靠一道长为a米的墙围一个矩形养鸡场(靠墙一面不用篱笆).

(1)、求下列情形下养鸡场的面积的最大值.
①a=15；②a =10 .

(2)、若可围成的矩形养鸡场的面积的最大值为67.5平方米，求a的值.

查看试题解析
22. 如图，已知，A，B是⊙O上的点，P为⊙O外一点，连结PA，PB，分别交⊙O于点C，D， $\overset{⌢}{A C} = \overset{⌢}{B D}$

(1)、求证：PA=PB；

(2)、若∠P=60， $\overset{⌢}{C D} = 3 \overset{⌢}{A C}$ ，△AOC的面积等于9，求图中阴影部分的面积.

查看试题解析
23. 如图，已知二次函数y=ax²+bx+c的图象经过点A(-1，0)，B(4，0)，E(1，3)，
与y轴交于点C.

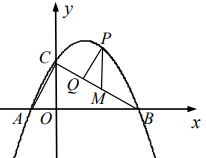(1)、求该二次函数表达式.

(2)、判断△ABC的形状，并说明理由.

(3)、Р为第一象限内该二次函数图象上一动点，过Р作PQllAC，交直线BC于点Q，作PM∥y轴交BC于M.
求证：
①△PQM $\sim$ △COA
②求线段PQ的长度的最大值.

查看试题解析
24. 如图，⊙O的半径为5，弦BC=6，A为BC所对优弧上一动点，△ABC的外角平分线AP交⊙O于点P，直线AP与直线BC交于点E.

(1)、如图1.①求证：点P为 $\overset{⌢}{B A C}$ 的中点；②求sin∠BAC的值.

(2)、如图2，若点A为 $\overset{⌢}{P C}$ 的中点，求CE的长.

(3)、若△ABC为非锐角三角形，求PA·AE的最大值.

查看试题解析