初中数学苏科版八年级下册第八章 认识概率 单元测试卷
试卷更新日期：2021-03-04 类型：单元试卷
一、单选题
-
1. 下列事件中，必然事件是（ ）A、随机抛掷一颗骰子，朝上的点数是6 B、今天考试小明能得满分 C、明天气温会升高 D、早晨的太阳从东方升起2. 下列说法中不正确的是（ ）A、抛掷一枚质量均匀的硬币，硬币落地时正面朝上是随机事件 B、把4个球放入三个抽屉中，其中一个抽屉至少有两个球是必然事件 C、为了呈现某个月的气温变化情况，应选择的统计图为扇形统计图 D、从一副扑克牌中任意抽取1张，摸到的牌是“A”的可能性比摸到的牌是“红桃”可能性小3. 某种产品10件，其中有2件次品，其余都是正品，今从中任取一件，抽到次品的可能性为（ ）A、一定 B、不可能 C、可能性较大 D、可能性较小4. 某校八年级(1)班共有学生50人，现在对他们的生日(可以不同年)进行统计，则下列正确的说法是（ ）.A、至少有两名学生生日相同 B、可能有两名学生生日相同 C、不可能有两名学生生日相同 D、肯定有两名学生生日相同5. 醴陵市“师生诗词大赛”成绩结果统计如表,成绩在91--100分的为优秀,则优秀的频率是（ ）
分数段
61—70
71--80
81--90
91--100
人数(人)
2
8
6
4
A、0.2 B、0.25 C、0.3 D、0.356. 一个布袋里装有4个红球、1个黄球和5个白球，除颜色外其它都相同。搅匀后任意摸出一个球，是红球的概率为（ ）A、 B、 C、 D、7. 设计一个摸球游戏，先在一个不透明的小盒子中放入 个白球，如果希望从中任意摸出一个球，是白球的概率为 ，那么应该向盒子中再放入多少个其他颜色的球（游戏用球除颜色外均相同）（ ）A、 B、 C、 D、8. 如图，在边长为1的小正方形网格中，△ABC的三个顶点均在格点上，若向正方形网格中投针，落在△ABC内部的概率是（ ）
A、 B、 C、 D、9. 老师组织学生做分组摸球实验．给每组准备了完全相同的实验材料，一个不透明的袋子，袋子中装有除颜色外都相同的3个黄球和若干个白球．先把袋子中的球搅匀后，从中随意摸出一个球，记下球的颜色再放回，即为一次摸球．统计各组实验的结果如下：一组
二组
三组
四组
五组
六组
七组
八组
九组
十组
摸球的次数
100
100
100
100
100
100
100
100
100
100
摸到白球的次数
41
39
40
43
38
39
46
41
42
38
请你估计袋子中白球的个数是（ ）
A、1个 B、2个 C、3个 D、4个10. 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果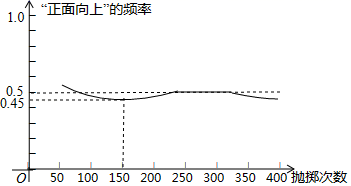
下面有三个推断：
①当抛掷次数是100时，计算机记录“正面向上”的次数是47，所以“正面向上”的概率是0.47；
②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5；
③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率一定是0.45．
其中合理的是（ ）
A、① B、② C、①② D、①③二、填空题
-
11. 袋中有5个黑球，3个白球和2个红球，每次摸一个球，摸出后再放回，在连续摸9次且9次摸出的都是黑球的情况下，第10次摸出红球的概率为 ．12. 转动如图的转盘（转盘中各个扇形的面积都相等），当它停止转动时，指针指向标有数字的区域的可能性最小.
13. 某种油菜籽在相同条件下发芽试验的结果如下：每批粒数
50
100
300
400
600
1000
发芽的频数
45
96
283
380
571
948
这种油菜籽发芽的概率的估计值是.（结果精确到0.01）
14. 一个不透明的袋子中，袋中有1 个红球，2 个白球和3 个黑球，这些球除颜色外均相同，将球摇匀后，从袋子中任意摸出一个球，摸到（填“红”或“白”或“黑”）球的可能性最大.15. 袋中有两个黄球、四个白球，三个绿球，它们称色外其它都一样，现从中任意出一个球，摸出绿球的概率是 ．16. 在一个不透明的口袋中，有大小、形状完全相同，颜色不同的球15个，从中摸出红球的概率为 ，则袋中红球的个数为 ．17. 在做“抛掷一枚质地均匀的硬币”试验时，下列说法正确的是.①不同次数的试验，正面向上的频率可能会不相同
②当抛掷的次数 很大时，正面向上的次数一定为
③多次重复试验中，正面向上发生的频率会在某个常数附近摆动，并趋于稳定
④连续抛掷 次硬币都是正面向上，第 次抛掷出现正面向上的概率小于
18. 小红通过一个设有红绿灯的十字路口时遇到红灯，这是 事件（填“随机”或“确定”）.19. 下列说法正确的是.①同角或等角的余角相等；②角是轴对称图形，角平分线是它的对称轴；③等腰三角形的平分线、底边上的中线、底边上的高重合，即“三线合一”；④必然事件发生的概率为1，不可能事件发生的概率为0.20. 在英语句子“Wish you success!”（祝你成功！）中任选一个字母，这个字母为“s”的概率为 ．三、综合题
-
21. 在一个不透明的口袋中装有大小、外形一模一样的5个红球.3个蓝球和2个白球，它们已经在口袋中被搅匀了,请判断以下是不确定事件、不可能事件还是必然事件.
(1)、从口袋中一次任意取出一个球,是白球.(2)、从口袋中一次任取5个球,全是蓝球.(3)、从口袋中一次任取5个球,只有蓝球和白球,没有红球.(4)、从口袋中一次任意取出6个球，恰好红、蓝、白三种颜色的球都齐了.22. 一只不透明的袋子中装有1个白球、2个黄球和3个红球，每个球除颜色外都相同，将球摇匀，从中任意摸出1个球．
（1）能够事先确定摸到的球的颜色吗？
（2）你认为摸到哪种颜色的球的概率最大？
（3）改变袋子中白球、黄球、红球的个数，使摸到这三种颜色的球的概率相等．
23. 一个不透明的袋中装有20个球，其中7个黄球，8个黑球，5个红球，这些球只有颜色不同，其它都相同．
(1)、求从袋中摸出一个球是黄球的概率；
(2)、现从袋中取出若干个黑球，搅匀后，使从袋中摸出一个球是黑球的概率是 ，求从袋中取出黑球的个数．
24. 一个口袋中放有16个球，其中红球6个，白球和黑球个若干个，每个球除了颜色外没有任何区别．(1)、小明通过大量反复的试验（每次将球搅匀后，任意摸出一个球记下颜色后再放回）发现，取出黑球的频率稳定在 附近，请你估计袋中白球的个数；(2)、若小明取出的第一个球是白色，将它放在桌上，闭上眼睛从袋中余下的球中再任意取出一个球，取出红球的概率是多少？25. 一只不透明的袋子中有2个红球、3个绿球和5个白球，这些球处颜色外都相同，将球搅匀，从中任意摸出1个球．(1)、会出现哪些可能的结果？(2)、能够确定摸到的一定是红球吗？(3)、你认为摸到哪种颜色的球可能性最大？哪种颜色的球可能性最小？(4)、怎样改变袋子中红球、绿球和白球的个数，使摸到这三种颜色的球的概率相同？26. 某校师生为了对学生零花钱的使用进行教育指导，对全班50名学生每人一周内的零花钱数额进行了调查统计，并绘制如下统计表：零花钱数额/元
5
10
15
20
学生人数/名
a
15
20
5
根据表格中信息，回答下列问题：
（1）求a的值．
（2）求着50名学生每人一周内零花钱数额的中位数．
（3）随机抽查一名学生，抽到一周内零花钱数额不大于10元的同学概率为多少？
27. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：摸球的次数
100
200
300
500
800
1000
3000
摸到白球的次数
65
124
278
302
481
599
1803
摸到白球的频率
0.65
0.62
0.593
0.604
0.601
0.599
0.601
(1)、请估计当 很大时，摸到白球的频率将会接近（精确到0.1）；(2)、假如摸一次，摸到黑球的概率 ；(3)、试估算盒子里黑颜色的球有多少只.28. 在一个不透明的口袋里装有若干个相同的红球，为了用估计袋中红球的数量，八（9）班学生在数学实验室分组做摸球实验：每组先将10个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复．下表是这次活动统计汇总各小组数据后获得的全班数据统计表：
(1)、按表格数据格式，表中的a=；b=；(2)、请估计：当次数s很大时，摸到白球的频率将会接近；
(3)、请推算：摸到红球的概率是（精确到0.1）；(4)、试估算：口袋中红球有多少只？