初中数学苏科版七年级下册第七章 平面图形的认识(二) 单元测试卷
试卷更新日期:2021-03-03 类型:单元试卷
一、单选题
-
1. 以下列各组线段为边,能组成三角形的是( )A、1cm,2cm,3cm B、3cm,4cm,5cm C、2cm,4cm,8cm D、5cm,6cm,14cm2. 下列说法中正确的有( )
①在同一平面内,不重合的两条直线若不相交,则必平行;②在同一平面内,不相交的两条线段必平行;③相等的角是对顶角;④两条直线被第三条直线所截,所得的同位角相等;⑤两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
A、1个 B、2个 C、3个 D、4个3. 以下四种作 边AC上的高,其中正确的作法是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,三角板的直角顶点落在矩形纸片的一边上.若 ,则 的度数是( )
4. 如图,三角板的直角顶点落在矩形纸片的一边上.若 ,则 的度数是( )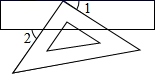 A、 B、 C、 D、5. 如果一个多边形的内角和是外角和的2倍,那么这个多边形是( )A、七边形 B、六边形 C、五边形 D、四边形6. 在下列条件中:① ,② ,③ ,④ 中,能确定 是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个7. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到 的位置,AB=8,DO=2,平移距离为4,则阴影部分面积为( )
A、 B、 C、 D、5. 如果一个多边形的内角和是外角和的2倍,那么这个多边形是( )A、七边形 B、六边形 C、五边形 D、四边形6. 在下列条件中:① ,② ,③ ,④ 中,能确定 是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个7. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到 的位置,AB=8,DO=2,平移距离为4,则阴影部分面积为( )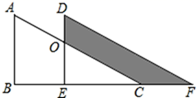 A、28 B、40 C、42 D、488. 如图, ,则下列等式正确的是( )
A、28 B、40 C、42 D、488. 如图, ,则下列等式正确的是( )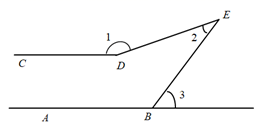 A、 B、 C、 D、9. 一副直角三角板叠放在一起可以拼出多种图形,如图①—④,每幅图中所求角度正确的个数有( )
A、 B、 C、 D、9. 一副直角三角板叠放在一起可以拼出多种图形,如图①—④,每幅图中所求角度正确的个数有( )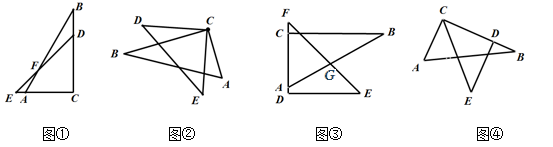
①∠BFD=15°;②∠ACD+∠ECB=150°;③∠BGE=45° ;④∠ACE=30°
A、1个 B、2个 C、3个 D、4个10. 如图,在 中, 、 、 分别为 、 、 的中点,且 ,则阴影部分的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
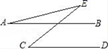
11. 六边形的内角和为°.12. 数轴上,将表示-1的点向右移动3个单位长度后,再向左移动5个单位长度,对应点表示的数是.13. 从一个多边形的一个顶点出发一共有7条对角线,则这个多边形的边数为.14. 若△ABC 的三个内角之比为 1:5:3,那么△ABC 中最大角的度数为 .15. 如图,若AB∥CD,∠C=60°,则∠A+∠E=度.
 16. 如图,有一块长为 、宽为 的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是 .
16. 如图,有一块长为 、宽为 的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是 .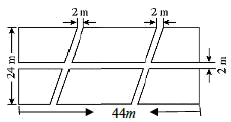 17. 如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于 .
17. 如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于 .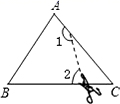 18. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=.
18. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=.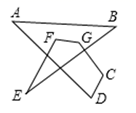
三、解答题
-
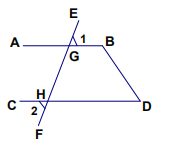
19. 如图,已知:∠1=∠2=70°,∠D=50°,求∠AGE 和∠B 的度数.
 20. 如图, 中,∠A=30°,∠B=70°,CE平分∠ACB交AB于点E,CD是AB边上的高,求:∠DCE的度数
20. 如图, 中,∠A=30°,∠B=70°,CE平分∠ACB交AB于点E,CD是AB边上的高,求:∠DCE的度数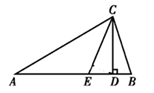 21. 如图,EF⊥BC于点F , ∠1=∠2,DG∥BA , 若∠2=40°,则∠BDG是多少度?
21. 如图,EF⊥BC于点F , ∠1=∠2,DG∥BA , 若∠2=40°,则∠BDG是多少度?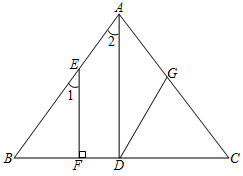 22. 如图,已知 , , , 平分 ,求 的度数.
22. 如图,已知 , , , 平分 ,求 的度数.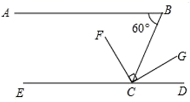 23. 如图,点F是△ABC的边BC延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF的度数.
23. 如图,点F是△ABC的边BC延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF的度数.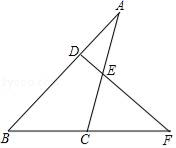 24. 如图,CD是△ABC的角平分线,点E是AC边上的一点, .
24. 如图,CD是△ABC的角平分线,点E是AC边上的一点, . (1)、求证: ;(2)、 , ,求∠DEC的度数.25. 如图,AB//DG,AD//EF.
(1)、求证: ;(2)、 , ,求∠DEC的度数.25. 如图,AB//DG,AD//EF.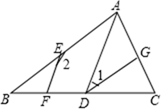 (1)、试说明:∠1+∠2=180°;(2)、若DG是∠ADC的平分线,∠2=138°,求∠B的度数.26. 如图,已知∠ABC=63°,∠ECB=117°.
(1)、试说明:∠1+∠2=180°;(2)、若DG是∠ADC的平分线,∠2=138°,求∠B的度数.26. 如图,已知∠ABC=63°,∠ECB=117°.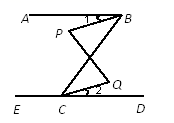 (1)、AB与ED平行吗,为什么;(2)、若∠P=∠Q,则∠1与∠2是否相等,说说你的理由.27. (概念认识)
(1)、AB与ED平行吗,为什么;(2)、若∠P=∠Q,则∠1与∠2是否相等,说说你的理由.27. (概念认识)如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的“三分线”.其中,BD是“邻AB三分线”,BE是“邻BC三分线”.
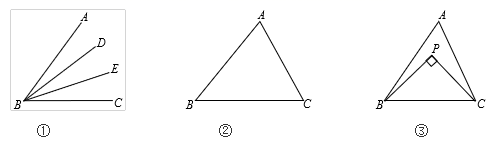 (1)、(问题解决)如图②,在△ABC中,∠A=70°,∠B=45°,若∠B的三分线BD交AC于点D,则∠BDC=°;(2)、如图③,在△ABC中,BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线,且BP⊥CP,求∠A的度数;(3)、(延伸推广)在△ABC中,∠ACD是△ABC的外角,∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P.若∠A=m°,∠B=n°,直接写出∠BPC的度数.(用含 m、n的代数式表示)28. (探究活动)(1)、问题发现:如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
(1)、(问题解决)如图②,在△ABC中,∠A=70°,∠B=45°,若∠B的三分线BD交AC于点D,则∠BDC=°;(2)、如图③,在△ABC中,BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线,且BP⊥CP,求∠A的度数;(3)、(延伸推广)在△ABC中,∠ACD是△ABC的外角,∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P.若∠A=m°,∠B=n°,直接写出∠BPC的度数.(用含 m、n的代数式表示)28. (探究活动)(1)、问题发现:如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC( )
∴∠C=∠CEF.( )
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C=( )(等量代换)
即∠B+∠C=∠BEC.
(2)、拓展探究:如果点E运动到图②所示的位置,其他条件不变,试探究∠B、∠C、∠BEC的数量关系并证明;(3)、解决问题:如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= . (直接写出结论,不用写计算过程)