初中数学湘教版九年级下册1.3不共线三点确定二次函数的表达式同步练习

试卷更新日期：2021-03-03 类型：同步测试

进入出卷网下载

一、单选题

1. 记某商品销售单价为x元，商家销售此种商品每月获得的销售利润为y元，且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时，他每月均可获得销售利润1800元；当商家将此种商品销售单价定为80元时，他每月可获得销售利润1550元，则y与x的函数关系式是（）

A、y＝﹣（x﹣60）²+1825 B、y＝﹣2（x﹣60）²+1850 C、y＝﹣（x﹣65）²+1900 D、y＝﹣2（x﹣65）²+2000

查看试题解析
2. 抛物线y＝ax²+bx﹣3与x轴交于A ， B两点，与y轴交于点C ，且OB＝OC＝3OA ，求抛物线的解析式（）

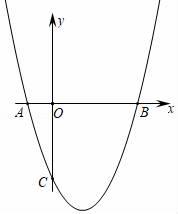A、y＝x²﹣2x﹣3 B、y＝x²﹣2x+3 C、y＝x²﹣2x﹣4 D、y＝x²﹣2x﹣5

查看试题解析
3. 二次函数 $y = a x^{2} + b x + c$ 经过点 $A (- 4 ， 0)$ 、 $B (- 1 ， 0)$ 和 $C (- 2 ， - 2)$ ，则下列说法正确的是 $($ $)$

A、抛物线的开口向下 B、当 $x > - 3$ 时， $y$ 随 $x$ 的增大而增大 C、二次函数的最小值是 $- 2$ D、抛物线的对称轴是直线 $x = - \frac{5}{2}$

查看试题解析
4. 若二次函数 $y = {ax}^{2} + bx + c$ 的x与y的部分对应值如下表，则当 $x = 1$ 时，y的值为 $($ 　　 $)$

x

$- 7$

$- 6$

$- 5$

$- 4$

$- 3$

$- 2$

y

$- 27$

$- 13$

$- 3$

3

5

3

A、5 B、 $- 3$ C、 $- 13$ D、 $- 27$

查看试题解析
5. 若抛物线经过 $(0, 1), (- 1, 0), (1, 0)$ 三点，则此抛物线的表达式为（）

A、 $y = - x^{2} + 1$ B、 $y = - x^{2} - 1$ C、 $y = x^{2} + 1$ D、 $y = x^{2} - 1$

查看试题解析
6. 已知二次函数 $y = a x^{2} + b x + c$ 的图象过点A（1，2），B（3，2），C（5，7）．若点M（-2，y₁），N（-1，y₂），K（8，y₃）也在二次函数 $y = a x^{2} + b x + c$ 的图象上，则下列结论正确的是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₃＜y₁＜y₂ D、y₁＜y₃＜y₂

查看试题解析

7. 已知抛物线

y = a x^{2} + b x + c

上部分点的横坐标

x

与纵坐标

y

的对应值如表：

$x$	···	-1	0	1	2	3	···
$y$	···	3	0	-1	$m$	3	···

有以下几个结论：①抛物线 $y = a x^{2} + b x + c$ 的开口向下；②抛物线 $y = a x^{2} + b x + c$ 的对称轴为直线 $x = - 1$ ；③方程 $a x^{2} + b x + c = 0$ 的根为0和2；④当 $y > 0$ 时，的取值范围是 $x < 0$ 或 $x > 2$ ；其中正确的是（）

A、①④ B、②④ C、③④ D、②③

查看试题解析

8. 已知点 $A (- 2, a)$ ， $B (\frac{1}{2}, b)$ ， $C (\frac{5}{2}, c)$ 都在二次函数 $y = - x^{2} + 2 x + 3$ 的图象上，那么a、b、c的大小关系是（）

A、 $a < b < c$ B、 $b < c < a$ C、 $c < b < a$ D、 $a < c < b$

查看试题解析
9. 已知点A（﹣1，5），B（0，0），C（4，0），D（2019，m），E（2020，n）在某二次函数的图象上.下列结论：①图象开口向上；②图象的对称轴是直线x＝2；③m＜n；④当0＜x＜4时，y＜0.其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
10. 在平面直角坐标系xOy中，四条抛物线如图所示，其解析式中的二次项系数一定小于1的是（）

A、y₁ B、y₂ C、y₃ D、y₄

查看试题解析

二、填空题

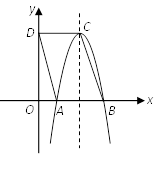
11. 某抛物线过点 $(- 1, 0)$ ， $(3, 0)$ ， $(0, - 3)$ ，则该抛物线解析式用一般式表示：

查看试题解析
12. 如图，平行四边形ABCD中， $A B = 4$ ，点 $D$ 的坐标是 $(0 ， 8)$ ，以点 $C$ 为顶点的抛物线经过 $x$ 轴上的点A ， B ，则此抛物线的解析式为．

查看试题解析
13. 已知二次函数 $y = a x^{2} + b x + c$ （ $a ， b ， c$ 是常数， $a \neq 0$ ）的y与x的部分对应值如下表：

x

-5

-4

-2

0

2

y

6

0

-6

-4

6

下列结论：

① $a > 0$ ；

②当 $x = - 2$ 时，函数最小值为 $- 6$ ；

③若点 $(- 8 ， y_{1})$ ，点 $(8 ， y_{2})$ 在二次函数图象上，则 $y_{1} < y_{2}$ ；

④方程 $a x^{2} + b x + c = - 5$ 有两个不相等的实数根．

其中，正确结论的序号是．（把所有正确结论的序号都填上）

查看试题解析
14. 已知二次函数 $y = 3 {(x - 1)}^{2} + k$ 的图象上有三点 $A (\sqrt{2}, y_{1})$ ， $B (2, y_{2})$ ， $C (- \sqrt{5}, y_{3})$ ，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系为．

查看试题解析
15. 已知抛物线y=ax²+bx+c(a≠0)经过点A(1，2)和B(-1，-6)两点，则a+c的值是

查看试题解析

三、解答题

16. 已知二次函数图象的最高点是A(1，4)，且经过点B(0，3)，与 $x$ 轴交于C、D两点(点C在点D的左侧).求△BCD的面积.

查看试题解析
17. 已知抛物线 $y = a x^{2} + b x + 1$ 经过点(1，﹣2)，(﹣2，13)．

(1)、求a ， b的值；

(2)、若(5， $y_{1}$ )，(m ， $y_{2}$ )是抛物线上不同的两点，且 $y_{2} = 12 - y_{1}$ ，求m的值．

查看试题解析
18. 嘉嘉给琪琪展示她做的一个小程序，如图，运行程序后屏幕显示一个平面直角坐标系，当她在键盘上输入数字“2”时，屏幕上显示一个点，坐标为 $(2 ， 0)$ ，输入数字“3”时，屏幕上显示另一个点，坐标为 $(3 ， - 3)$ ，嘉嘉告诉琪琪：这些点都在抛物线 $y = a x^{2} + b x$ 上．

(1)、求抛物线的解析式，并求出输入“4”得到的点的坐标；

(2)、嘉嘉和琪琪从2、3、4中各选一个数字输入，得到两个不同的点，求两个点都在 $x$ 轴下方的概率．

查看试题解析

x	$- 7$	$- 6$	$- 5$	$- 4$	$- 3$	$- 2$
y	$- 27$	$- 13$	$- 3$	3	5	3

初中数学湘教版九年级下册1.3不共线三点确定二次函数的表达式 同步练习

一、单选题

二、填空题

三、解答题

初中数学湘教版九年级下册1.3不共线三点确定二次函数的表达式同步练习