高中数学人教A版(2019)必修二 6.3 平面向量基本定理及坐标表示 课后测试
试卷更新日期:2021-03-03 类型:同步测试
一、单选题
-
1. 已知向量 ,则 ( )A、 B、 C、 D、2. 已知向量 ,若 ,则实数 的值为( )A、2 B、-2 C、3 D、-33. 已知 是单位向量, ,若平面向量 满足 , 且 ,则 ( )A、9 B、8 C、7 D、64. 已知平面向量 , ,则向量 的模是A、
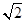 B、
C、
B、
C、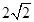 D、5
5. 已知 , , ,则 ( )A、5 B、7 C、9 D、116. 向量 , 满足| |=1,| |=2, 与 的夹角为60°,则|2 |=( )A、2 B、2 C、4 D、27. 已知向量 ,若 ,则 ( )A、1或4 B、1或-4 C、-1或4 D、-1或-48. 已知 , 是夹角为 的两个单位向量,则 与 的夹角是( )A、60° B、120° C、30° D、90°
D、5
5. 已知 , , ,则 ( )A、5 B、7 C、9 D、116. 向量 , 满足| |=1,| |=2, 与 的夹角为60°,则|2 |=( )A、2 B、2 C、4 D、27. 已知向量 ,若 ,则 ( )A、1或4 B、1或-4 C、-1或4 D、-1或-48. 已知 , 是夹角为 的两个单位向量,则 与 的夹角是( )A、60° B、120° C、30° D、90°二、多选题
-
9. 设向量 , ,则( )A、 B、 C、 D、 与 的夹角为10. 已知向量 , , ,设 , 的夹角为 ,则( ).A、 B、 C、 D、11. 已知平面向量 , , 满足 .若 ,则 的值可能为( )A、 B、-2 C、0 D、12. 已知向量 , ,若向量 ,则可使 成立的 可能是 ( )A、(1,0) B、(0,1) C、(−1,0) D、(0,−1)
三、填空题
-
13. 已知向量 ,且 ,则 .14. 已知平面向量 , 满足 , 与 的夹角为120°,则 的最大值是.15. 若 与 平行,则实数m=.
四、解答题
-
16. 已知向量 满足: .(1)、求 与 的夹角;(2)、求 .17. 在平面直角坐标系 中,设向量 , , .(1)、若 ,求 的值;(2)、设 , ,且 ,求 的值.18. 已知向量 ,k、t为正实数, .(1)、若 求k的最大值;(2)、是否存在k、t使得 ?若存在,求出k的取值范围,若不存在,请说明理由.

