高中数人教A版必修5 第一章解三角形单元测试卷

试卷更新日期：2021-03-03 类型：单元试卷

进入出卷网下载

一、单选题

1. 在 $△ A B C$ 中， $B = \frac{π}{3}$ ， $C = \frac{π}{4}$ ， $A B = 2$ ，则 $A C =$ （）

A、 $\sqrt{3}$ B、 $\sqrt{6}$ C、3 D、 $3 \sqrt{3}$

查看试题解析
2. $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，且 $a = 1$ ， $c = \sqrt{3}$ ， $B = \frac{π}{6}$ ，则 $△ A B C$ 的面积为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{3}}{4}$ C、 $\frac{\sqrt{3}}{2}$ 或 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{2}$ 或 $\frac{\sqrt{3}}{4}$

查看试题解析
3. $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，若 $b^{2} = a c$ ， $c = 2 a$ ，则 $\cos C =$ （）．

A、 $\frac{\sqrt{2}}{4}$ B、 $\frac{3}{4}$ C、 $- \frac{\sqrt{2}}{4}$ D、 $- \frac{3}{4}$

查看试题解析
4. 在 $△ A B C$ 中， $△ A B C$ 的面积为S， $4 S = \sqrt{3} (a^{2} + c^{2} - b^{2})$ ， $\vec{A B} \cdot \vec{B C} = - 2$ ，且满足 $sin A + sin C = 2sin B$ ，则该三角形的外接圆的半径R为（）

A、 $\frac{4 \sqrt{3}}{3}$ B、 $\frac{2 \sqrt{3}}{3}$ C、 $\sqrt{3}$ D、2

查看试题解析
5. 一艘海轮从A处出发，以每小时40海里的速度沿南偏东40°的方向直线航行，30分钟后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是（）

A、10 $\sqrt{2}$ 海里 B、10 $\sqrt{3}$ 海里 C、20 $\sqrt{3}$ 海里 D、20 $\sqrt{2}$ 海里

查看试题解析
6. 在 $Δ A B C$ 中，若 $b^{2} + c^{2} = a^{2} + b c$ ，则 $A =$ （）

A、30° B、45° C、60° D、120°

查看试题解析
7. $△ A B C$ 内角 $A$ ， $B$ ， $C$ 的对边分别是 $a$ ， $b$ ， $c$ ，已知 $a \cos B + b \cos A = - 4 c \cos C$ ， $a = 3$ ， $c = 4$ ，则 $b =$ （）

A、 $\frac{3}{2}$ B、2 C、3 D、 $\frac{7}{2}$

查看试题解析
8. 在 $△ A B C$ 中，若 $\sin A = \frac{\sqrt{2}}{2}$ ，则 $\cos B + \sqrt{2} \cos C$ 的取值范围是（）

A、 $(0 ， 1]$ B、 $(0 ， 1] \cup (2 ， \sqrt{5}]$ C、 $(0 ， 1] \cup (\frac{3}{2} \sqrt{2} ， \sqrt{5}]$ D、以上答案都不对

查看试题解析

二、多选题

9. 在 $△ A B C$ 中，内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ .根据下列条件解三角形，其中有两解的是（）

A、 $b = 10 ， A = 45 ° ， C = 70 °$ B、 $b = 45 ， c = 48 ， B = 60 °$ C、 $a = 14 ， b = 16 ， A = 45 °$ D、 $a = 7 ， b = 5 ， A = 80 °$

查看试题解析
10. 在 $△ A B C$ 中，角A，B，C的对边分别是a，b，c，若 $a = \sqrt{10} ， a^{2} + b^{2} - c^{2} = a b \sin C$ ， $a \cos B + b \sin A = c$ ，则下列结论正确的是（）

A、 $\tan C = 2$ B、 $A = \frac{π}{4}$ C、 $b = \sqrt{2}$ D、 $△ A B C$ 的面积为6

查看试题解析
11. 在 $△ A B C$ 中，角 $A$ 、 $B$ 、 $C$ 的对边分别是 $a$ 、 $b$ 、 $c$ ．下面四个结论正确的是（）

A、 $a = 2$ ， $A = 30 °$ ，则 $△ A B C$ 的外接圆半径是4 B、若 $\frac{a}{\cos A} = \frac{b}{\sin B}$ ，则 $A = 45 °$ C、若 $a^{2} + b^{2} < c^{2}$ ，则 $△ A B C$ 一定是钝角三角形 D、若 $A < B$ ，则 $\cos A < \cos B$

查看试题解析
12. 在 $Δ A B C$ 中，角A，B，C所对的边分别为a，b，c，且 $(a + b) ： (a + c) ： (b + c) = 9 ： 10 ： 11$ ，则下列结论正确的是（）

A、 $\sin A ： \sin B ： \sin C = 4 ： 5 ： 6$ B、 $Δ A B C$ 是钝角三角形 C、 $Δ A B C$ 的最大内角是最小内角的2倍 D、若 $c = 6$ ，则 $Δ A B C$ 外接圆半径为 $\frac{8 \sqrt{7}}{7}$

查看试题解析

三、填空题

13. 在 $△ A B C$ 中， $\cos C = \frac{2}{3}$ ， $A C = 4$ ， $B C = 3$ ，则 $\sin B =$ .

查看试题解析
14. 在 $△ A B C$ 中，已知 $A C = 1$ ， $∠ A$ 的平分线交 $B C$ 于 $D$ ，且 $A D = 1$ ， $B D = \sqrt{2}$ ，则 $△ A B C$ 的面积为.

查看试题解析
15. 在 $Δ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c ， b \tan B + b \tan A = - 2 c \tan B$ ，且 $a = 8$ ， $Δ A B C$ 的面积为 $4 \sqrt{3}$ ，则 $b + c$ 的值为．

查看试题解析
16. 如图，在四边形ABCD中， $∠ D = 2 ∠ B$ ， $A D = 2 D C = 4$ ， $\sin ∠ B = \frac{3}{4}$ ， $\sin ∠ C A B \cdot \sin ∠ A C B = \frac{9}{22}$ ，则 $△ A B C$ 的面积为.

查看试题解析

四、解答题

17. 如图， $D$ 是直角 $△$ $A B C$ 斜边 $B C$ 上一点， $A C = \sqrt{3} D C$ ．

(1)、若 $∠ D A C = 30 °$ ，求角 $B$ 的大小；

(2)、若 $B D = 2 D C$ ，且 $D C = 3 ，$ 求 $A D$ 的长．

查看试题解析
18. $△ A B C$ 中内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ， $a \cos (B - C) + a \cos A = 2 \sqrt{3} b \sin C \cos A$ .

(1)、求角 $A$ ；

(2)、若 $△ A B C$ 的周长为 $4 \sqrt{3} + 3$ ，外接圆半径为 $\sqrt{3}$ ，求 $△ A B C$ 的面积.

查看试题解析
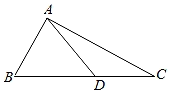19. 目前，中国已经建成全球最大的5G网络，无论是大山深处还是广袤平原，处处都能见到5G基站的身影.如图，某同学在一条水平公路上观测对面山项上的一座5G基站AB，已知基站高 $A B = 50 m$ ，该同学眼高1.5m（眼睛到地面的距离），该同学在初始位置C处（眼睛所在位置）测得基站底部B的仰角为37°，测得基站顶端A的仰角为45°.

参考数据： $\sin 8 ° \approx 0.14$ ， $\sin 37 ° \approx 0.6$ ， $\sin 45 ° \approx 0.7$ ， $\sin 127 ° \approx 0.8$ .

(1)、求出山高BE（结果保留整数）；

(2)、如图，当该同学面向基站AB前行时（保持在同一铅垂面内），记该同学所在位置M处（眼睛所在位置）到基站AB所在直线的距离 $M D = x m$ ，且记在M处观测基站底部B的仰角为 $α$ ，观测基站顶端A的仰角为 $β$ .试问当 $x$ 多大时，观测基站的视角 $∠ A M B$ 最大?

查看试题解析
20. 在锐角 $△ A B C$ 中，角 $A$ 、 $B$ 、 $C$ 所对的边分别为 $a$ 、 $b$ 、 $c$ ，已知 $c \cdot \cos B = b \cdot (1 - \cos C)$ .
（Ⅰ）求证 $a = b$ ；

（Ⅱ）求 $\cos C - \sin A$ 的取值范围.

查看试题解析
21. 在 $△ A B C$ 中，角A，B，C所对的边分别为a，b，c，且 $a \sin B - b \cos C = c \cos B$ ．

(1)、判断 $△ A B C$ 的形状．

(2)、若 $f (x) = \sin x + \sqrt{3} \cos x$ ，求 $f (A)$ 的取值范围．

查看试题解析
22. 已知 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别是 $a$ ， $b$ ， $c$ ，且 $a^{2} = b^{2} + b c$ ．

(1)、求证： $A = 2 B$ ；

(2)、若 $B = \frac{π}{6}$ ， $b = 2$ ，点 $P$ 为 $△ A B C$ 所在平面内一动点，且满足 $\vec{A P} \cdot \vec{C P} = 0$ ，当线段 $B P$ 的长度取得最小值时，求 $△ A P C$ 的面积．

查看试题解析

高中数人教A版必修5 第一章 解三角形 单元测试卷

一、单选题

二、多选题

三、填空题

四、解答题

高中数人教A版必修5 第一章解三角形单元测试卷