山东省武城县2020-2021学年九年级上学期数学期末试卷
试卷更新日期：2021-03-02 类型：期末考试
一、选择题(本大题共12个小题每小题4分，共48分。)
-
1. 下面四个图形分别是绿色食品、节水、节能和回收标志，在这四个标志中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 已知关于x的一元二次方程3x2+4x-5=0，下列说法正确的是（ ）A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、没有实数根。 D、无法确定3. 今年元旦期间，某种女服装连续两次降价处理，由每件200元调至72元，设平均每次的降价百分率为x，则得方程（ ）A、200(1-x)=72×2 B、200(1-x%)2 =72 C、200(1-x)2=72 D、200x2=724. 如图所示，在4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1 ， 则其旋转中心是（ ）
A、点A B、点B C、点C D、点D5. 函数y=-2x2先向右平移1个单位，再向下平移2个单位，所得函数解析式是（ ）A、y=-2(x-1)2+2 B、y=-2 (x-1)2-2 C、y=-2(x+1)2+2 D、y=-2(x+1)2-26. 已知二次函数y=ax2+bx+c的图象如图所示，则在同一直角坐标系中，一次函数y=ax+b和反比例函数y= 的图象大致是（ ）
A、
B、
C、
D、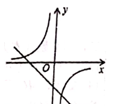
7. 直角三角形的两边长分别为16和12，则此三角形的外接圆半径是（ ）A、8或6 B、10或8 C、10 D、88. 一个圆锥的侧面积是底面积的3倍，则圆锥侧面展开图的扇形的圆心角是（ ）A、120° B、180° C、240° D、300°9. 如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为 ，点A ， B ， E在x轴上，若正方形BEFG的边长为12，则C点坐标为（ ）
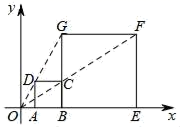A、（6，4） B、（6，2） C、（4，4） D、（8，4）10. 如图是二次函数y=ax2+bx+c的部分图象，使y≥-1成立的x的取值范围是（ ）
A、x≥-1 B、x≤-1 C、-1≤x≤3 D、x≤-1或x≥311. 在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为(1，0)，顶点A的坐标(0，2)，顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C"的坐标为（ ）
A、( ，0) B、(2，0) C、( ，0) D、(3，0)12. 如图，已知直线y= x-3与x轴、y轴分别交于A，B两点，P是以C(0，1)为圆心，1为半径的圆上一动点，连接PA，PB，则△PAB面积的最大值是（ ）
A、8 B、12 C、 D、二、填空题(本大题共6个小题，每小题4分，共24分)
-
13. 一元二次方程4x(x-2)=x-2的解为。14. 如图，AC是⊙O的切线，切点为C，BC是⊙O的直径，AB交⊙O于点D，连接OD，若∠A=50°，则∠COD的度数为 ．
15. 在某一时刻，测得一根长为1.5m的标杆的影长为3m，同时测得一根旗杆的影长为 26m，那么这根旗杆的高度为m。16. 甲、乙两位同学各抛掷一枚质地均匀的骰子，他们抛掷的点数分别记为a、b，则a+b=9的概率为 ．17. 如图，A、B、C、D是⊙O上四个点，连接OA、0C，过A作AE⊥OC交圆周于点E，连接OE，若∠ABC=140°，则∠OEA的度数为。
18. 已知二次函数y=ax2+bx+c的图象如图所示，则下列结论：①a<0，c>0，b<0 ；②b2-4ac>0； ③a+b>am2+bm(m为实数)；④b+2a=0；⑤-a+c>0 正确的有。
三、解答题(本大题有7小题，共78分)
-
19.(1)、解方程：x2-5x+6=0(2)、用配方法解方程：-x2-2x+3=020. 在如图所示的方格纸中，每个小方格都是边长为1个单位的正方形，AABC的三个顶点都在格点上(每个小方格的顶点叫格点)。
(1)、画出△ABC关于点O中心对称的△A1B1C1；(2)、将△ABC绕点O顺时针旋转90°，画出旋转后的△A2B2C2 ， 并求线段BC扫过的面积。21. 小颖和小亮都想去观看“垃圾分类”宣传演出，但只有一张入场券，于是他们设计了一个“配紫色”游戏：A，B是两个可以自由转动的转盘，每个转盘都被分成面积相等的几个扇形、同时转动两个转盘，如果其中一个转盘转出了红色，另一个转盘转出了蓝色，那么可以配成紫色．若配成紫色，则小颖去观看，否则小亮去观看．这个游戏对双方公平吗？请说明理由．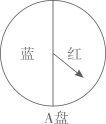
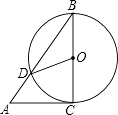
22. 已知：A是以BC为直径的圆上的一点，BE是⊙O的切线，CA的延长线与BE交于E点，F是BE的中点，延长AF，CB交于点P．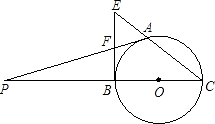
(1)、求证：PA是⊙O的切线；(2)、若AF=3，BC=8，求AE的长．23. 为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒．
(1)、试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；
(2)、当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？
(3)、为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得不低于6000元的利润，那么超市每天至少销售粽子多少盒？
24. 如图，点D，E分别是ABC的边AC，AB上的点，且∠ADE=∠B，其中AE=1.5，AC=2，BC=2，求DE的长。
25. 如图，抛物线y=ax2+bx-3交x轴于A、B两点，交y轴于C点点D为抛物线顶点，连接BD，点P为线段BD上一动点，作PE⊥x轴，垂足为E，连接PC，EC，已知抛物线对称轴为直线x=1，点A坐标为(-1，0)。
(1)、求抛物线的解析式；(2)、设△PCE的面积为S，请问在点P的移动过程中S是否存在最大值，若存在，请求出S最大值以及此时点P的坐标，若不存在，请说明理由；(3)、在线段BD上存在一点Q，使得△CDQ为等腰三角形，请直接写出点Q的坐标。