广东省阳江市三区联考2020-2021学年九年级上学期数学期末试卷
试卷更新日期：2021-03-02 类型：期末考试
一、选择题(每题3分，共30分)
-
1. 下列方程一定是一元二次方程的是（ ）A、3x2+ -1=0 B、5x2-6y-3= 0 C、ax2-x+2=0 D、3x2-2x-1=02. 某种物体的三视图是如图的三个图，那么该物体的形状是（ ）
A、圆柱体 B、圆锥体 C、立方体 D、长方体3. 若函数是反比例函数，则m的值等于（ ）A、1 B、±1 C、 D、-14. 用配方法解方程m2-3m=4，应将方程两边同时（ ）A、加上 B、加上 C、减去 D、减去5. 已知△ABC∽△A1B1C1 ， 且AB=3， AC=5，A1C1=15，则A1B1=（ ）A、9 B、1 C、6 D、36. 在一个不透明的盒子里有2个红球和n个白球，这些球除了颜色外其余完全相同，摇匀后随机摸出一个，摸到红球的概率是 ，则n的值为（ ）A、3 B、5 C、8 D、107. 在△ABC中，∠A=105°，∠B=45°，则tanC的值是（ ）A、 B、 C、1 D、8. 在方格中，在标有序号①②③④的小正方形中选一个涂黑，使其与图形阴影部分构成中心对称图形该小正方形的序号是（ ）
A、① B、② C、③ D、④9. 如图，AB是⊙O的弦，半径OC⊥AB于点D，若⊙O的半径为5，AB=8，则CD的长是（ ）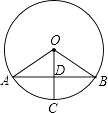
A、2 B、3 C、4 D、510. 已知二次函数y=ax2+bx+c的图像如图所示，那么abc，b2 -4ac，2a+b，a+b+c这四个代数式中，值为正数的有（ ）
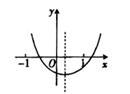A、4个 B、3个 C、2个 D、1个二、填空题(每题4分，共28分)
-
11. 若将方程x2+6x=7化为（x+m）2=16，则m=.12. 如图，点A，B，C在⊙O上，∠ABO=32°，∠ACO=38°，则∠BOC=。
13. 两道单项选择题都含有A，B，C，D四个选项，瞎猜这两道题，恰好全部猜对的概率为 。14. 如图，已知A点是反比例函数y= (k≠0，x>0)的图像上一点，AB⊥x轴于B，且△ABO的面积为5，则k的值为 。
15. 如图，在△ABC中，AB=8，AC=6，点D在AC上，且AD=2，如果要在AB上找一点E，使△ADE与△ABC相似，那么AE=。
16. 如图，已知⊙O的两条弦AC，BD相交于点E，∠A=70°，∠C=50°，那么tan∠AEB= 。
17. 某种商品每件进价20元，调查表明：在某段时间内以每件x元(20≤x≤30，且x为整数)出售，可卖出(30-x)件。若使利润最大，则每件的售价应为 。三、解答题一(每题6分，共18分)
-
18. 用公式法解方程：2x2-4x-1=019. 已知关于x的反比例函数y=(m-2)xm2-5(1)、求m的值；(2)、它的图像位于哪些象限?20. 如今，“垃圾分类” 意识已深入人心，垃圾一般可分为：可回收垃圾、厨余垃圾、有害垃圾、其他垃圾．其中甲投放-袋垃圾，乙投放两袋垃圾。(1)、求出甲投放的垃圾恰好是厨余垃圾的概率；(2)、求乙投放的两袋垃圾是不同类别的概率。
四、解答题二(每题8分，共24分)
-
21. 某数学兴趣小组的同学在一次数学活动中， 为了测量某建筑物AB的高，他们来到与建筑物AB在同一平地且相距12m的建筑物CD上的C处观察，测得某建筑物顶部A的仰角为30°、底部B的俯角为45°。求建筑物AB的高。(精确到1m，可供选用的数据： ≈1.4， ≈1.7)
22. 商场出售一批进价为2元的贺卡，在市场营销中发现此商品日销售单价x (元)与日销售量y (张) 之间有如下关系：x/元
3
4
5
6
y /张
20
15
12
10
(1)、根据表中的数据在平面直角坐标系中描出实数对(x，y)的对应点；(2)、猜想并确定y关于x的函数解析式，并画出函数图象；(3)、设经营此贺卡的日销售利润为W (元)，试求出W关于x的函数解析式，若物价局规定此贺卡的日销售单价最高不能超过10元/张，请你求出当日销售单价x定为多少元时，才能获得最大日销售利润？23. 将两块大小相同的含30°角的直角三角板(∠BAC=∠B'A'C= 30° )按图①方式放置，固定三角板A'B'C，然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90° )至图②所示的位置，AB与A'C交于点E；AC与A'B'交于点F，AB与A'B'相交于点O。
(1)、求证：△BCE≌△B'CF。(2)、当旋转角等于30°时，AB 与A'B'垂直吗？请说明理由。五、解答题三(每题10分，共20分)
-
24. 如图，已知⊙O的半径为1，DE是⊙O的直径，过D作⊙O的切线AD，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形。
(1)、求AD的长；(2)、BC是⊙O的切线吗？若是，给出证明，若不是，说明理由。25. 如图，已知一次函数y= x+2的图像与x轴交于点A，与二次函数的图象交于y轴上的一点B，另一交点为D，二次函数图象的顶点C在x轴的正半轴上，且OC=2。
(1)、求二次函数的表达式；(2)、设P为x轴上的一个动点，当△PBD为直角三角形，且Rt△PBD面积最小时，求点P的坐标；(3)、当0≤x≤2时，抛物线的一段BC上是否存在一点Q，使点Q到直线AD的距离等于 ？若存在，请求出此时点Q的坐标；若不存在，请说明理由。