广东省韶关市乐昌市2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-03-02 类型:期末考试
一、选择题:(本大题共 10小题,每小题2分,共20分)
-
1. 下列汽车标志图案,其中是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 下列运算中正确的是( )A、a2·a3=a5 B、(a2)3=a5 C、a6÷a2=a3 D、a5+a5=2a103. 下列长度的三条线段能组成三角形的是( )A、 B、 C、 D、4. 已知am=3,an=4,则am+n的值为( )A、7 B、12 C、 D、5. 在平面直角坐标系XOY中,点P(-2,3)关于x轴的对称点坐标是( )A、(-2,-3) B、(2,-3) C、(2,3) D、(-3,-2)6. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、
A、1个 B、2个 C、3个 D、4个2. 下列运算中正确的是( )A、a2·a3=a5 B、(a2)3=a5 C、a6÷a2=a3 D、a5+a5=2a103. 下列长度的三条线段能组成三角形的是( )A、 B、 C、 D、4. 已知am=3,an=4,则am+n的值为( )A、7 B、12 C、 D、5. 在平面直角坐标系XOY中,点P(-2,3)关于x轴的对称点坐标是( )A、(-2,-3) B、(2,-3) C、(2,3) D、(-3,-2)6. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、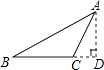 B、
B、 C、
C、 D、
D、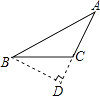 7. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D,如果CE=12,则ED的长为( )
7. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D,如果CE=12,则ED的长为( ) A、3 B、4 C、5 D、68. 如图,将两根钢条AA'、BB’的中点O连在一起,使AA’、BB'能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A'B'的长等于内槽宽AB,那么判定△OAB≌△OA' B'的理由是( )
A、3 B、4 C、5 D、68. 如图,将两根钢条AA'、BB’的中点O连在一起,使AA’、BB'能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A'B'的长等于内槽宽AB,那么判定△OAB≌△OA' B'的理由是( ) A、SAS B、ASA C、SSS D、AAS9. 已知等腰三角形的一边长为4,另一边长为8,则它的周长是( ).A、 B、 C、 D、 或10. 如图,AD是△ABC的中线,E,P分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌OCDE;④BF∥CE;⑤CE=AE。其中正确的是( )
A、SAS B、ASA C、SSS D、AAS9. 已知等腰三角形的一边长为4,另一边长为8,则它的周长是( ).A、 B、 C、 D、 或10. 如图,AD是△ABC的中线,E,P分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌OCDE;④BF∥CE;⑤CE=AE。其中正确的是( ) A、①② B、③⑤ C、①③④ D、①④⑤
A、①② B、③⑤ C、①③④ D、①④⑤二、填空题(本大题共7小题,每小题3分,共21分)
-
11. 在显微镜下测得“新冠”病毒的直径为0.0000002050米,用科学记数法表示为米。12. 若分式 有意义,则x的取值范围是 .13. 因式分解:x2-y2= .14. 计算:( )-1-20210=。15. 计算: 的结果是 .16. 已知等腰三角形的一个内角为50°,那么该等腰三角形的另外两个角的度数分别为。17. 如图,△ABC中,AB=6,AC=7,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于E、F,则△AEF的周长为。

三、解答题(本大题共3小题,每小题6分,共18分)
-
18. 化简:19. 如图,点B、E、C、F在同一直线上,∠A=∠D,∠B=∠DEF,AB=DE,求证: BE=CF。
 20. 先化简,再求值: y(x+y)+(x+))(x-y)-x2 , 其中x=-2,y= 。
20. 先化简,再求值: y(x+y)+(x+))(x-y)-x2 , 其中x=-2,y= 。四、解答题(本大题共3小题,每小题7分,共21分)
-
21. 如图,在△ABC中,∠C=90°。
 (1)、作∠BAC的平分线AD,交BC于D;(2)、若AB=10cm,CD=4cm,求△ABD的面积。22. 某车间按计划要生产450个零件,由于改进了生产设备,该车间实际每天生产的零件数比原计划每天多生产20%,结果提前5天完成任务,求该车间原计划每天生产的零件个数?23. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)、作∠BAC的平分线AD,交BC于D;(2)、若AB=10cm,CD=4cm,求△ABD的面积。22. 某车间按计划要生产450个零件,由于改进了生产设备,该车间实际每天生产的零件数比原计划每天多生产20%,结果提前5天完成任务,求该车间原计划每天生产的零件个数?23. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.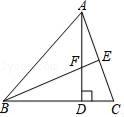 (1)、若∠BAC=60°,∠C=70°,求∠AFB的大小;(2)、若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.
(1)、若∠BAC=60°,∠C=70°,求∠AFB的大小;(2)、若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.五、解答题(本大题共2小题,每小题10分,共20分)

