山东省德州市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-02 类型：期末考试

进入出卷网下载

一、选择题(每小题4分，共48分)

1. 下面的图形中对称轴最多的是（）

A、 B、 C、 D、

查看试题解析
2. 在 $\frac{1}{x}$ ， $\frac{1}{2}$ ， $\frac{3 x y}{π}$ ， $\frac{3}{x + y}$ ， $a + \frac{1}{m}$ ，中分式的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 已知多边形的每个内角都是108°，则这个多边形是（）

A、五边形 B、七边形 C、九边形 D、不能确定

查看试题解析
4. 已知等腰三角形两边长是8cm和4cm，那么它的周长是（　　）

A、12cm B、16cm C、16cm或20cm D、20cm

查看试题解析
5. 下列运算正确的是（）

A、a³·a⁴=a¹² B、(a³)²=a⁵ C、(3a²)³=27a⁶ D、a⁶^÷a³=a²

查看试题解析
6. 下列条件不能判定两个直角三角形全等的是（）

A、两条直角边对应相等 B、斜边和一锐角对应相等 C、斜边和一直角边对应相等 D、两个锐角对应相等

查看试题解析
7. 多项式3x-9，x²-9与x²-6x+9的公因式为（）

A、x+3 B、(x+3)² C、x-3 D、x²+9

查看试题解析
8. 化简 $(1 - \frac{2}{x + 1}) \div \frac{1}{x^{2} - 1}$ 的结果是（）

A、(x+1)² B、(x-1)² C、 $\frac{1}{{(x + 1)}^{2}}$ D、 $\frac{1}{{(x - 1)}^{2}}$

查看试题解析
9. 如图在△MBC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于D，如果△ADE的周长为6cm， AC=4cm，那么AD等于（）

A、2cm B、4cm C、3cm D、6cm

查看试题解析
10. 如图，在△ABC中，AB边上的高为（）

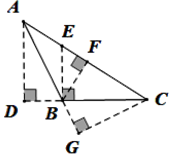A、CG B、BF C、BE D、AD

查看试题解析
11. 等边三角形的两个内角平分线所成的锐角是（）

A、30° B、50° C、60° D、90°

查看试题解析
12. 每年的10月17日设为“扶贫日”，当天某校八年级两个班举行了募捐活动，各班均捐款1800元。已知2班比1班人均捐款多4元，2班的人数比1班的人数少10%，设1班有x人，可列分式方程为（）

A、 $\frac{1800}{(1 - 10 %)} = \frac{1800}{x} + 4$ B、 $\frac{1800}{x + 4} = (1 - 10 %) \frac{1800}{x}$ C、 $\frac{1800}{(1 + 10 %)} = \frac{1800}{x} + 4$ D、 $\frac{1800}{x + 4} = (1 + 10 %) \frac{1800}{x}$

查看试题解析

二、填空题(每小题4分，共24分)

13. 当时，分式 $\frac{x}{x - 1}$ 有意义：当时，分式 $\frac{x + 2}{x - 3}$ 值为零。

查看试题解析
14. 已知P₁(a-1，5)和P₂(2，b-1)关于x轴对称，则-(a+b)²⁰¹⁸的值为。

查看试题解析
15. 若2^x=3，8^y=6，则2^x+3y的值为。

查看试题解析
16. 因式分解：3x²-12=。

查看试题解析
17. 如图，△ABC中，∠ACB=90°，∠A=15°，AB边的垂直平分线DE交AC于D，交AB于E，若AD=10cm，则BC长为_。

查看试题解析
18. 如图，在Rt△ABC和Rt△DCB中已知∠A=∠D=90°，若利用“HL"证明△ABC≌△DCB，可添加的条件是。(不添加字母和辅助线)

查看试题解析

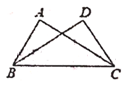
三、解答题(本大题共7小题，共78分)

19. 解下列分式方程：

(1)、 $\frac{3}{x - 1} = \frac{2}{x - 1} + 1$ ；

(2)、 $\frac{5}{x - 2} - \frac{3}{x^{2} - 4} = \frac{1}{2 - x}$

查看试题解析
20. 在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，△ABC的顶点均在格点上，点A的坐标是(-3，-1)。

(1)、将△ABC沿y轴正方向平移3个单位得到△A₁B₁C₁ ，画出△A₁B₁C₁ ，并写出点B₁的坐标：

(2)、西出△ABC关于y轴对称的△A₂B₂C₂ ，并写出点C₂的坐标：[和(1)画在同一个图中]

(3)、求△MBC的面积。

查看试题解析
21. 先化简： $\frac{3 - a}{2 a - 4} \div (a + 2 - \frac{5}{a - 2})$ ，再从2，-2，3，-3中选一个合适的数作为a的值代入求值。

查看试题解析
22.

(1)、已知a+b=5，ab= $- \frac{1}{4}$ 。求下列各式的值：①a²+b²；②(a-b)²

(2)、若x+ $\frac{3}{2}$ y- 2z+1=0，求9^x·27^y÷81的值。

查看试题解析
23. 已知，如图，AB=AD，∠B=∠D，∠1=∠2=60°。

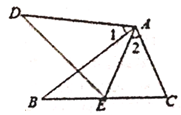(1)、求证：△ADE≌△ABC

(2)、求证：AE=CE

查看试题解析
24. 为防控新冠肺炎，某药店用1000元购进若干医用防护口罩，很快售完，接着又用2500元购进第二批口罩，已知第二批所购口罩的数量是第一批所购口罩数的2倍，且每只口罩的进价比第一批的进价多 0.5元。求第一批口罩每只的进价是多少元？

查看试题解析
25. 先阅读下面的内容，再解决问题：
例题；若m²+2mn+2n²-6n+9=0，求m和n的值。

解：因为m²+2mn+2n²-6n+9=0，

所以m²+2mn+n²+n²-6n+9=0，

所以(m+n)²+ (n-3)²=0，

所以m+n=0，n-3=0，

所以m=-3，n=3．

问题；

(1)、若x²+2y²-2xy+6y+9=0，求x的值；

(2)、已知a，b，c是△ABC的三边长，满足a²+b²=6a+8b-25。且c是△ABC中最长的边，求c的取值范围。

查看试题解析