山西省朔州市怀仁市2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2021-03-02 类型：期中考试

进入出卷网下载

一、单选题

1. -5的倒数是（）

A、5 B、-5 C、 $\frac{1}{5}$ D、 $- \frac{1}{5}$

查看试题解析
2. 一个两位数，十位上的数字是 $a$ ，个位上的数字是 $b$ ，则这个两位数是（）

A、 $a b$ B、a+b C、 $10 a b$ D、 $10 a + b$

查看试题解析
3. 有理数 $a$ 、 $b$ 在数轴上的位置如图所示，那么下列式子中不成立的是（）

A、 $a > b$ B、 $a < 1$ C、 $a b < 0$ D、 $b < 1$

查看试题解析
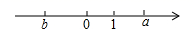4. 已知 $a + 2 b = 3$ ，则整式 $2 (2 a - 3 b) - 3 (a - 3 b) - b$ 的值为（）．

A、-3 B、3 C、-6 D、6

查看试题解析
5. 2020年是不平凡的一年，新冠肺炎疫情在武汉爆发，据有关部门初步统计，国家已经投入资金1390亿进行抗疫防控，这个数据的背后不仅是抗击疫情的强力保障，更是祖国综合实力的直接体现，为此很多人高呼：此生无悔入华夏，来世再做中国人．将1390亿用科学记数法表示（）

A、 $1.39 \times 10^{3}$ B、 $1.39 \times 10^{8}$ C、 $1.39 \times 10^{11}$ D、 $1390 \times 10^{8}$

查看试题解析
6. 下面的结论正确的是（）

A、0不是单项式 B、5²abc是五次单项式 C、－4和4是同类项 D、3m²n³－3m³n²=0

查看试题解析
7. 下列说法正确的是（）

A、0.720精确到百分位 B、5.078×10⁴精确到千分位 C、36万精确到个位 D、2.90×10⁵精确到千位

查看试题解析
8. 下列结论中，正确的是（）．

A、单项式 $\frac{3 x y^{2}}{7}$ 的系数是3，次数是2 B、单项式 $m$ 的次数是1，没有系数 C、单项式 $- x y^{2} z$ 的系数是-1，次数是4 D、多项式 $2 x^{2} + x y + 3$ 是三次三项式

查看试题解析

9. 下列每个表格中的四个数都是按相同的规律填写的，根据此规律确定 x 的值为（）

1	4		2	6		3	8		4	10		…		$a$	20
2	9		3	20		4	35		5	54		…		$b$	$x$

A、135 B、170 C、209 D、252

查看试题解析

10. 各个数位上数字的立方和等于其本身的三位数叫做“水仙花数”．例如153是“水仙花数”，因为 $1^{3} + 5^{3} + 3^{3} = 153$ ．以下四个数中是“水仙花数”的是（）

A、135 B、220 C、345 D、407

查看试题解析

二、填空题

11. 8的相反数是．

查看试题解析
12. 2020年1月1日零点，北京、上海、宁夏、重庆的气温分别是 $- 4 ° C$ 、 $5 ° C$ 、 $6 ° C$ 、 $- 8 ° C$ ，当时这四个城市中，气温最低的是．

查看试题解析
13. 三个连续偶数中间的一个数是2n，那么它们的和等于．

查看试题解析
14. 若 $\frac{1}{5} x^{3} y^{2 k + 1}$ 与 $- \frac{2}{3} x^{3} y^{9}$ 是同类项，则 $k =$ ．

查看试题解析
15. 某轮船顺水航行了 $4 h$ ，逆水航行了 $2 h$ ，已知船在静水中的速度为 $x km/h$ ，水流速度为 $y km/h$ ，则此轮船共航行了 $km$ ．

查看试题解析
16. 要使关于x，y的多项式 $m y^{3} + 3 n x^{2} y + 2 y^{3} - x^{2} y + y$ 不含三次项，则 $2 m + 3 n$ 的值为．

查看试题解析
17. 某校园餐厅把wifi密码做成了数学题，小亮在餐厅就餐时，思索了一会儿，输入密码，顺利地连接到了学子餐厅的网络，那么他输入的密码是．
账号：Xue Zi Can Ting

5★3★2=151025

9★2★4=183654

8★6★3=482472

7★2★5=密码

查看试题解析
18. 试写出一个只含字母 $x$ ， $y$ 的多项式，且满足下列条件：（1）四次三项式；（2）每一项的系数均为1或-1；（3）不含常数项；（4）每一项必须同时含字母 $x$ ， $y$ ，且不能含其他字母．这个多项式可以是．

查看试题解析

三、解答题

19. 计算

(1)、 $30 - (- 12) - 18 + (- 10)$

(2)、 $- 3^{2} \times 2 + 3 \times {(- 2)}^{2}$

(3)、 $(\frac{1}{8} - \frac{5}{12}) \times 24 - {(- 3 - 3)}^{2} \div {(- 6 \div 3)}^{2}$

查看试题解析
20. 化简

(1)、 $4 a - [- 3 a - (- 7 a)]$

(2)、 $3 a^{2} - 4 a b + [a^{2} - 2 (a^{2} - 3 a b)]$

查看试题解析
21. 先化简，再求值： $5 (4 a^{2} - 2 a b^{3}) - 4 (5 a^{2} - 3 a b^{3})$ ，其中 $a = - 1$ ， $b = 2$ ．

查看试题解析
22. 已知： ${(a + 2)}^{2} + | b - 1 | + {(c - 2)}^{2} = 0$ ，求 ${(a - b + c)}^{3}$ 的值．

查看试题解析
23. 对于下列式子，根据要求回答问题：
$2 x + y$ ， $- 2 x^{2} + \frac{1}{2} + x y$ ， $\frac{1}{3}$ ， $- \frac{x y^{3}}{6}$ ， $\frac{1}{x}$ ， $\frac{1}{π}$ ， $x^{3} y^{5}$ ， $\frac{4}{5} x^{3} + 0.2 x^{2} - x$ ， $2 x^{2} y - x^{3} y - x y^{3} - 5$ ， $- x y + x^{2} - 1$

(1)、单项式有：﹔其中次数为4的单项式是，它的系数为．

(2)、找出四次多项式是；将此多项式按字母 $x$ 的降幂排列为．

(3)、请找出所有的二次三项式，并求出它们的和．

查看试题解析
24. 操作探究：已知在纸面上有一数轴（如下图所示）左右折叠纸面，折痕所在的直线与数轴的交点为“对折中心点”．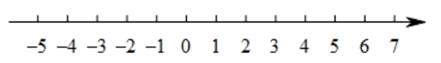

(1)、操作一：
左右折叠纸面，使表示1的点与表示-1的点重合，则表示-3的点与表示的点重合；

(2)、操作二：
左右折叠纸面，使表示-1的点与表示3的点重合，回答以下问题：

①“对折中心点”所表示的数为，对折后表示5的点与表示的点重合；

②若数轴上 $A$ ， $B$ 两点之间的距离为12（ $A$ 在 $B$ 的左侧），且 $A$ ， $B$ 两点经折叠后重合，则 $A$ 点表示的数是， $B$ 点表示的数是．

查看试题解析
25. 如图，小明有5张写有不同数字的卡片，请你按题目要求抽取卡片，完成问题：

(1)、从中抽取2张卡片，使这两张卡片上的数字的乘积最大，如何抽取？最大值是多少？

(2)、从中抽取2张卡片，使这两张卡片上的数字的商最小，如何抽取？最小值是多少？

(3)、从中抽取4张卡片，用学过的运算方法，使计算结果为24，如何抽取？试写出一个算式．

查看试题解析