福建省三明市大田县2020-2021学年七年级上学期数学期中试卷
试卷更新日期:2021-03-02 类型:期中考试
一、单选题
-
1. 下列几何体都是由平面围成的是( )A、圆柱 B、圆锥 C、四棱柱 D、球2. 下列各数中,比-1小的数是( ).A、 B、-2 C、0.1 D、3. 用一个平面去截一个几何体,截面不可能是圆的几何体的是( )A、
 B、
B、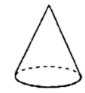 C、
C、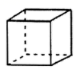 D、
D、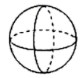 4. 某市决定为全市中小学教室安装空调,今年预计投入资金136000000元,其中数字136000000用科学记数法可表示为( ).A、 B、 C、 D、5. 某正方体的每个面上都有一个汉字.它的一种平面展开图如图所示,那么在原正方体中,与“筑”字所在面相对的面上的汉字是( )
4. 某市决定为全市中小学教室安装空调,今年预计投入资金136000000元,其中数字136000000用科学记数法可表示为( ).A、 B、 C、 D、5. 某正方体的每个面上都有一个汉字.它的一种平面展开图如图所示,那么在原正方体中,与“筑”字所在面相对的面上的汉字是( ) A、抗 B、疫 C、长 D、城6. 下列各式中,符合代数书写规则的是( )A、 B、 C、 D、7. 下列各组单项式中,不是同类项的是( )A、3与-2 B、 与 C、 与 D、 与8. 下面去括号正确的是( )A、 B、 C、 D、9. 下列各组数中,互为相反数的一组是( )A、 与 B、 与 C、 与 D、 与10. 按如图的“数值转换机”计算:若开始输入的 值为1,计算 的值最后输出的结果是( ).
A、抗 B、疫 C、长 D、城6. 下列各式中,符合代数书写规则的是( )A、 B、 C、 D、7. 下列各组单项式中,不是同类项的是( )A、3与-2 B、 与 C、 与 D、 与8. 下面去括号正确的是( )A、 B、 C、 D、9. 下列各组数中,互为相反数的一组是( )A、 与 B、 与 C、 与 D、 与10. 按如图的“数值转换机”计算:若开始输入的 值为1,计算 的值最后输出的结果是( ). A、3 B、7 C、15 D、31
A、3 B、7 C、15 D、31二、填空题
-
11. 的倒数是.12. 在0、-1.5、-2、3这四个数中,属于负分数的是 .13. 单项式 的次数是 .14. 一种零件的直径尺寸在图纸上是30±0.03(单位:mm),它表示这种零件的标准尺寸是30mm,加工要求尺寸最大不超过mm.15. 小明有5张写着不同数字的卡片,卡片上的数字分别是 、 、0、3、4,从中抽出2张卡片,用学过的加、减、乘、除、乘方中的一种运算方法进行运算,使结果最大,算式为 .16. “24”点游戏,游戏规则:用一副扑克牌去掉大小王,从中任取4张,将抽出的数进行加减乘除四则运算,使其结果为24,如:1、2、3、4,可运算为 现抽3、-4、2、5,用上述规则写出运算等式使其结果为24,等式可以是 .
三、解答题
-
17. 计算:(1)、 .(2)、 .(3)、(4)、 .18. 一架飞机进行特技表演,第一次上升 ,第二次上升 ,第三次下降 ,第四次又下降 (记升为正,下降为负).(1)、这时飞机在初始位置的上方还是下方?相距初始位置多少米?(2)、飞机在表演中共运行了多少米?19. 化简与求值:(1)、化简: ;(2)、先化简再求值:已知 , ,求 的值.其中 , .20. 有理数 、 在数轴上如图,
 (1)、在数轴上表示 、 ;(2)、试把这 、 、0、 、 五个数按从小到大用“<”连接;(3)、用>或<填空: ;(4)、化简: .21. 如图,是由7个大小相同的小立方块搭成的一个几何体.
(1)、在数轴上表示 、 ;(2)、试把这 、 、0、 、 五个数按从小到大用“<”连接;(3)、用>或<填空: ;(4)、化简: .21. 如图,是由7个大小相同的小立方块搭成的一个几何体.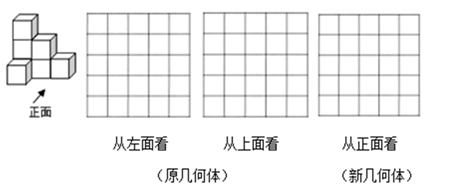 (1)、请在指定位置画出该几何体从左面、上面看到的形状图;(2)、小颖从该几何体中移去一个小立方块,变成由6个大小相同的小立方块搭成的一个几何体.发现所得新几何体与原几何体相比,从左面、上面看到的形状图仍然保持不变,请画出新几何体从正面看到的形状图.22. 用棋子按规律摆出下列一组图形:
(1)、请在指定位置画出该几何体从左面、上面看到的形状图;(2)、小颖从该几何体中移去一个小立方块,变成由6个大小相同的小立方块搭成的一个几何体.发现所得新几何体与原几何体相比,从左面、上面看到的形状图仍然保持不变,请画出新几何体从正面看到的形状图.22. 用棋子按规律摆出下列一组图形: (1)、填写下表:
(1)、填写下表:图形编号
1
2
3
4
5
图中棋子数
5
8
11
(2)、照这样的方式摆下去,则第 个图形中棋子的枚数是;(3)、照这样的方式摆下去,则第100个图形中棋子的枚数是 .23. 今年秋季,斗门土特产喜获丰收,某土特产公司组织10辆汽车装运甲,乙,丙三种土特产去外地销售,按计划10辆车都要装运,每辆汽车只能装运同一士特产,且必须装满,设装运甲种士特产的汽车有x辆,装运乙种特产的汽车有y辆,根据下表提供的信息,解答以下问题:土特产种类
甲
乙
丙
每辆汽车运载量(吨)
4
3
6
每吨土特产获利(元)
1000
900
1600
(1)、装运丙种土特产的车辆数为辆(用含有x , y的式子表示);(2)、用含有x , y的式子表示这10辆汽车共装运土特产的数量;(3)、求销售完装运的这批土特产后所获得的总利润(用含有x , y的式子表示).24. 我们知道, ,类似地,若我们把 看成一个整体,则 .这种解决问题的方法渗透了数学中的“整体思想”,“整体思想”是中学教学解题中的一种重要的思想方法,其应用极为广泛.请运用“整体思想”解答下面的问题:(1)、把 看成一个整体,计算 的结果是( ).A、 B、 C、 D、(2)、已知 ,求代数式 的值;(3)、已知 , , ,求 的值.25. 已知如图,在数轴上有 , 两点,所表示的数分别为 , ,点 以每秒5个单位长度的速度向右运动,同时点 以每秒3个单位长度的速度也向右运动,如果设运动时间为 秒,解答下列问题: (1)、运动前线段 的长为;运动1秒后线段 的长为;(2)、运动 秒后,点 运动的路程为(用含 的代数式表示),此时,点 表示为;(用含 的代数式表示)(3)、求 时,点 与点 恰好重合;(4)、在上述运动的过程中,是否存在某一时刻 ,使得线段 的长为5,若存在,求 的值;若不存在,请说明理由.
(1)、运动前线段 的长为;运动1秒后线段 的长为;(2)、运动 秒后,点 运动的路程为(用含 的代数式表示),此时,点 表示为;(用含 的代数式表示)(3)、求 时,点 与点 恰好重合;(4)、在上述运动的过程中,是否存在某一时刻 ,使得线段 的长为5,若存在,求 的值;若不存在,请说明理由.