山西省朔州市怀仁市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-03-02 类型:期中考试
一、单选题
-
1. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列方程中,关于x的一元二次方程是( )A、 B、 C、 D、3. 将抛物线 向左平移2个单位,再向下平移3个单位,所得抛物线是( )A、 B、 C、 D、4. , , 是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、5. 函数y=ax2﹣a与y=ax﹣a(a≠0)在同一坐标系中的图象可能是( )A、
2. 下列方程中,关于x的一元二次方程是( )A、 B、 C、 D、3. 将抛物线 向左平移2个单位,再向下平移3个单位,所得抛物线是( )A、 B、 C、 D、4. , , 是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、5. 函数y=ax2﹣a与y=ax﹣a(a≠0)在同一坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( )
6. 如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( ) A、30° B、40° C、50° D、60°7. 设 、 、 是 三边,并且关于 的方程 有两个相等的实数根,判断 的形状,正确的结论是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、正三角形8. 如图,四边形 内接于 ,若 ,则 的度数为( )
A、30° B、40° C、50° D、60°7. 设 、 、 是 三边,并且关于 的方程 有两个相等的实数根,判断 的形状,正确的结论是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、正三角形8. 如图,四边形 内接于 ,若 ,则 的度数为( ) A、 B、 C、 D、9. 如图,抛物线 经过点 ,与 轴交于 ,抛物线的对称轴为直线 ,则下列结论中:① ;②方程 的解为-1和3;③ ;④ ,其中正确的结论有( )
A、 B、 C、 D、9. 如图,抛物线 经过点 ,与 轴交于 ,抛物线的对称轴为直线 ,则下列结论中:① ;②方程 的解为-1和3;③ ;④ ,其中正确的结论有( )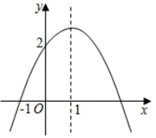 A、1个 B、2个 C、3个 D、4个10. 欧几里得的《原本》记载,形如 的方程的图解法是:画 ,使 , , ,再在斜边 上截取 .则该方程的一个正根是( )
A、1个 B、2个 C、3个 D、4个10. 欧几里得的《原本》记载,形如 的方程的图解法是:画 ,使 , , ,再在斜边 上截取 .则该方程的一个正根是( )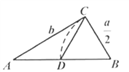 A、 的长 B、 的长 C、 的长 D、 的长
A、 的长 B、 的长 C、 的长 D、 的长二、填空题
-
11. 如果关于x的二次函数 与x轴只有1个交点,则 .12. 若 ,则 .13. 廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为 ,为保护廊桥的安全,在该抛物线上距水面 高为8米的点 , 处要安装两盏警示灯,则这两盏灯的水平距离 是米.
 14. 如图,半径为5的圆O中,AB、DE是互相垂直的两条弦,垂足为P , 且AB=ED=8,则OP= .
14. 如图,半径为5的圆O中,AB、DE是互相垂直的两条弦,垂足为P , 且AB=ED=8,则OP= . 15. 如图,在 中, , , 为 边上的高,动点 在 上,从点 出发,沿 方向运动,设 , 的面积为 ,矩形 的面积为 , ,则y与x的关系式是 .
15. 如图,在 中, , , 为 边上的高,动点 在 上,从点 出发,沿 方向运动,设 , 的面积为 ,矩形 的面积为 , ,则y与x的关系式是 .
三、解答题
-
16.(1)、解方程:(2)、解方程: .17. △ABC在平面直角坐标系xOy中的位置如图所示.
 (1)、作△ABC关于点C成中心对称的△A1B1C1 .(2)、将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2 .(3)、在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)18. 已知关于x的方程x2+mx+m-2=0.(1)、若此方程的一个根为1,求m的值;(2)、求证:不论m取何实数,此方程都有两个不相等的实数根.19. 已知抛物线y=ax2-2ax+c与x轴交于A,B两点,与y轴正半轴交于点C,且A(-1,0).(1)、一元二次方程ax2-2ax+c=0的解是;(2)、一元二次不等式ax2-2ax+c>0的解集是;(3)、若抛物线的顶点在直线y=2x上,求此抛物线的解析式.20. 某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?21. 如图,正方形ABCD中,E、F分别在边BC、CD上,且∠EAF=45°,连接EF , 这种模型属于“半角模型”中的一类,在解决“半角模型”问题时,旋转是一种常用的分析思路.例如图中△ADF与△ABG可以看作绕点A旋转90°的关系.这可以证明结论“EF=BE+DF”,请补充辅助线的作法,并写出证明过程.
(1)、作△ABC关于点C成中心对称的△A1B1C1 .(2)、将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2 .(3)、在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)18. 已知关于x的方程x2+mx+m-2=0.(1)、若此方程的一个根为1,求m的值;(2)、求证:不论m取何实数,此方程都有两个不相等的实数根.19. 已知抛物线y=ax2-2ax+c与x轴交于A,B两点,与y轴正半轴交于点C,且A(-1,0).(1)、一元二次方程ax2-2ax+c=0的解是;(2)、一元二次不等式ax2-2ax+c>0的解集是;(3)、若抛物线的顶点在直线y=2x上,求此抛物线的解析式.20. 某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?21. 如图,正方形ABCD中,E、F分别在边BC、CD上,且∠EAF=45°,连接EF , 这种模型属于“半角模型”中的一类,在解决“半角模型”问题时,旋转是一种常用的分析思路.例如图中△ADF与△ABG可以看作绕点A旋转90°的关系.这可以证明结论“EF=BE+DF”,请补充辅助线的作法,并写出证明过程.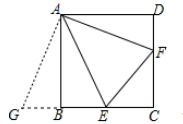 (1)、延长CB到点G , 使BG= , 连接AG;(2)、证明:EF=BE+DF22. 2016年3月国际风筝节在铜仁市万山区举办,王大伯决定销售一批风筝,经市场调研:蝙蝠形风筝进价每个为10元,当售价为每个12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请解答以下问题:(1)、用表达式表示蝙蝠形风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);(2)、王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?(3)、当售价定为多少时,王大伯获得利润最大,最大利润是多少?23. 在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)、延长CB到点G , 使BG= , 连接AG;(2)、证明:EF=BE+DF22. 2016年3月国际风筝节在铜仁市万山区举办,王大伯决定销售一批风筝,经市场调研:蝙蝠形风筝进价每个为10元,当售价为每个12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请解答以下问题:(1)、用表达式表示蝙蝠形风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);(2)、王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?(3)、当售价定为多少时,王大伯获得利润最大,最大利润是多少?23. 在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.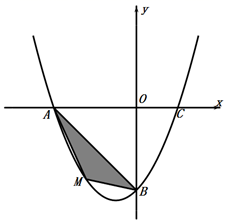 (1)、求抛物线的解析式;(2)、若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.(3)、若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、 O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
(1)、求抛物线的解析式;(2)、若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.(3)、若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、 O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.