山西省临汾市侯马市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-03-02 类型:期中考试
一、单选题
-
1. 在下列四组线段中,成比例线段的是( )A、3、4、5、6 B、5、15、2、6 C、4、8、3、5 D、8、4、1、32. 一元二次方程x2﹣6x﹣5=0配方可变形为( )A、(x﹣3)2=14 B、(x﹣3)2=4 C、(x+3)2=14 D、(x+3)2=43. 下面计算正确的是( )A、 B、 C、 D、4. 如图, ABC中,DE∥BC,AD:BD=1:3,则OE:OB=( )
 A、1:3 B、1:4 C、1:5 D、1:65. 一元二次方程根与系数之间的关系最早由一位法国数学家发现,并以他的名字命名了这个定理.这位数学家是16世纪最有影响的数学家之一,被尊称为“代数学之父”,他是第一个引进系统的代数符号,并对方程论做了改进,他就是( )A、祖冲之 B、韦达 C、笛卡尔 D、欧几里得6. 今年“国庆节”和“中秋节”双节期间,某微信群规定,群内的每个人都要发一个红包,并保证群内其他人都能抢到且自己不能抢自己发的红包,若此次抢红包活动,群内所有人共收到90个红包,则该群一共有( )
A、1:3 B、1:4 C、1:5 D、1:65. 一元二次方程根与系数之间的关系最早由一位法国数学家发现,并以他的名字命名了这个定理.这位数学家是16世纪最有影响的数学家之一,被尊称为“代数学之父”,他是第一个引进系统的代数符号,并对方程论做了改进,他就是( )A、祖冲之 B、韦达 C、笛卡尔 D、欧几里得6. 今年“国庆节”和“中秋节”双节期间,某微信群规定,群内的每个人都要发一个红包,并保证群内其他人都能抢到且自己不能抢自己发的红包,若此次抢红包活动,群内所有人共收到90个红包,则该群一共有( )
A、9人 B、10人 C、11人 D、12人7. 如图所示,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为( ) A、5米 B、6米 C、8米 D、10米8. x=-2是关于x的一元二次方程2x2+3ax-2a2=0的一个根,则a的值为( )A、1或4 B、-1或-4 C、-1或4 D、1或-49. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分AC,点 H 为垂足,设 AB=x,AD=y,则y 关于x 的函数关系用图象大致可以表示为 ( )
A、5米 B、6米 C、8米 D、10米8. x=-2是关于x的一元二次方程2x2+3ax-2a2=0的一个根,则a的值为( )A、1或4 B、-1或-4 C、-1或4 D、1或-49. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分AC,点 H 为垂足,设 AB=x,AD=y,则y 关于x 的函数关系用图象大致可以表示为 ( )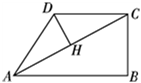 A、
A、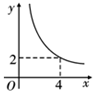 B、
B、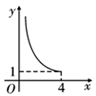 C、
C、 D、
D、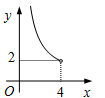
二、填空题
-
10. 已知5a=6b(a≠0),那么 的值为 .11. 当0<x<4时,化简 的结果是.12. 已知x1和x2是方程2x2-5x+1=0的两个根,则 的值为 .13. 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D是AC中点,过点D作DE⊥AC交BC于点E,则CE的长度是 .
 14. 如图,△ABC中,D在AC上,且AD:DC=1:n,E为BD的中点,AE的延长线交BC于F,那么FC:BF的值为(用含有n的代数式表示).
14. 如图,△ABC中,D在AC上,且AD:DC=1:n,E为BD的中点,AE的延长线交BC于F,那么FC:BF的值为(用含有n的代数式表示).
三、解答题
-
15.(1)、(2)、16. 解下列方程:(1)、(x+3)(x-1)=4x-4;(2)、2x2-20x+25=0.17. 作图题:如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
 (1)、画出位似中心点O;(2)、△A'B'C'与△ABC的位似比是;(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A'B'C'关于点O中心对称的△A"B"C",并直接写出△A"B"C"各顶点的坐标.18. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)、画出位似中心点O;(2)、△A'B'C'与△ABC的位似比是;(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A'B'C'关于点O中心对称的△A"B"C",并直接写出△A"B"C"各顶点的坐标.18. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.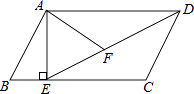 (1)、求证:△ADF∽△DEC;
(1)、求证:△ADF∽△DEC;
(2)、若AB=8,AD=6 ,AF=4 ,求AE的长.
19. 关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、当 取满足条件的最大整数时,求方程的根.20. 观察下列各式: ,, ,…
(1)、猜想① .② , 其中n为正整数.
(2)、计算:21. 某商场新上市一款运动鞋,每双进货价为150元,投入市场后,调研表明:当销售价为200元时,平均每天能售出10双;而当销售价每降低5元时,平均每天就能多售出5双.(1)、商场要想尽快回收成本,并使这款运动鞋的销售利润平均每天均达到675元,那么这款运动鞋的销售价应定为多少元?(2)、请用配方法求:这款运动鞋的销售价定为多少元时,可使商场平均每天获得的利润最大?最大利润是多少元?22. (如图,在平面直角坐标系中,直线 与 轴、 轴分别交于A、B两点,动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,当其中一点到达终点时,另一点也随之停止运动.设点P运动的时间为t(秒). (1)、直接写出A、B两点的坐标.(2)、当△APQ与△AOB相似时,求t的值.(3)、设△APQ的面积为S(平方单位),求S与t之间的函数关系式.
(1)、直接写出A、B两点的坐标.(2)、当△APQ与△AOB相似时,求t的值.(3)、设△APQ的面积为S(平方单位),求S与t之间的函数关系式.