福建省三明市大田县2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-03-02 类型：期中考试

进入出卷网下载

一、单选题

1. 在平行四边形 $A B C D$ 中， $∠ A : ∠ B = 2 : 1$ ，则 $∠ B$ 的度数（）

A、120° B、60° C、30° D、150°

查看试题解析
2. 用配方法解一元二次方程 $x^{2} - 4 x - 9 = 0$ ，可变形为（）

A、 ${(x - 2)}^{2} = 9$ B、 ${(x - 2)}^{2} = 13$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x + 2)}^{2} = 13$

查看试题解析
3. 布袋中装有除颜色外没有其他区别的1个红球和2个白球，搅匀后从中摸出一个球，放回搅匀，再摸出第二个球，两次都摸出白球的概率是（）

A、 $\frac{4}{9}$ B、 $\frac{2}{9}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
4. 已知：四条线段成比例线段1，2，6，m，则第四比例项m的值是（）

A、4 B、8 C、12 D、9

查看试题解析
5. 如图，直线l₁∥l₂∥l₃ ， AB＝3，BC＝6，DE＝2，则EF的长是（）

A、4 B、5 C、6 D、7

查看试题解析
6. 在小孔成像问题中，如图所示，若为O到AB的距离是18cm，O到CD的距离是6cm，则像CD的长是物体AB长的（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、2倍 D、3倍

查看试题解析
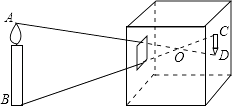7. 电影《我和我的祖国》讲述了普通人与国家之间息息相关的动人故事.一上映就获得全国人民的追捧，第一天票房约3亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达10亿元，若把平均每天票房的增长率记作x，则可以列方程为（）

A、 $3 (1 + x) = 10$ B、 $3 {(1 + x)}^{2} = 10$ C、 $3 + 3 {(1 + x)}^{2} = 10$ D、 $3 + 3 (1 + x) + 3 {(1 + x)}^{2} = 10$

查看试题解析
8. 如图，已知： $Δ A B C ∽ Δ D A C$ ， $∠ B = 36 °$ ， $∠ D = 117 °$ ， $∠ B A D$ 的度数为（）

A、 $36 °$ B、 $117 °$ C、 $143 °$ D、 $153 °$

查看试题解析
9. 如图，四边形 $A B C D$ 中， $∠ A = 90 °$ ， $A B = 2 \sqrt{3}$ ， $A D = 2$ ，点 $M$ ， $N$ 分别为线段 $B C$ ， $A B$ 上的动点（含端点，但点 $M$ 不与点 $B$ 重合），点 $E$ ， $F$ 分别为 $D M$ ， $M N$ 的中点，则 $E F$ 长度的最大值为（）

A、3 B、 $2 \sqrt{3}$ C、4 D、2

查看试题解析
10. 如图，在矩形 $A B C D$ 中， $E$ ， $F$ 分别为边 $B C$ ， $C D$ 的中点，线段 $A E$ ， $A F$ 与对角线 $B D$ 分别交于点 $M$ ， $N$ ．设矩形 $A B C D$ 的面积为 $S$ ，则以下4个结论中：① $A M ： M E = 2 ： 1$ ；② $B M ： M N ： N D = 1 ： 1 ： 1$ ；③ $S_{1} + S_{3} + S_{5} = \frac{1}{3} S$ ；④ $S_{2} ： S_{4} ： S_{6} = 2 ： 1 ： 1$ ．正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知 $\frac{m}{n} = \frac{2}{5}$ ，那么 $\frac{m}{m + n} =$ ．

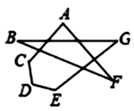
查看试题解析
12. 一个池塘中放养一些草鱼若干，现想测算一下池塘中草鱼的总条数，小明在池塘中放入60条红鲫鱼，一周后，小明在池塘中捞出200条鱼中有5条是红鲫鱼，把鱼全部放回池塘中．请你猜测池塘中现在大约有条草鱼．

查看试题解析
13. 如果关于 $x$ 的一元二次方程 $a x^{2} + b x - 1 = 0$ 的一个解是 $x = 1$ ，则 $2021 - a - b =$ .

查看试题解析
14. 如图， $∠ A + ∠ B + ∠ C + ∠ D + ∠ E + ∠ F$ +∠G= ．

查看试题解析
15. 关于 $x$ 的方程 $(m + 1) x^{2} + 3 x - 1 = 0$ 有两个实数根，则 $m$ 的取值范围是.

查看试题解析
16. 如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝7，BC＝10，则EF的长为.

查看试题解析

三、解答题

17. 用适当的方法解一元二次方程：

(1)、 ${(x - 2)}^{2} = 9$ ；

(2)、 $x^{2} + 2 x - 3 = 0$ ．

查看试题解析
18. 在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (1 ， - 2)$ ， $B (2 ， - 1)$ ， $C (4 ， - 3)$ ．

(1)、画出 $△ A B C$ 关于 $x$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、以点 $O$ 为位似中心，在网格中画出 $△ A_{1} B_{1} C_{1}$ 的位似图形 $△ A_{2} B_{2} C_{2}$ ，使 $△ A_{2} B_{2} C_{2}$ 与 $△ A_{1} B_{1} C_{1}$ 的相似比为 $2 ： 1$ ；

(3)、设点 $P (a ， b)$ 为 $△ A B C$ 内一点，则依上述两次变换后点 $P$ 在 $△ A_{2} B_{2} C_{2}$ 内的对应点 $P_{2}$ 的坐标是．

查看试题解析
19. 如图，菱形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于 $O$ ， $E$ 是 $B C$ 中点，连接 $O E$ 并延长到 $F$ ，使 $E F = O E$ ．求证：四边形 $O B F C$ 是矩形．

查看试题解析
20. 求证：相似三角形对应边上的角平分线之比等于相似比．

要求：

(1)、根据给出的 $△ A B C$ 及线段 $A^{'} B^{'}$ ， $∠ A^{'}$ （ $∠ A^{'} = ∠ A$ ），以线段 $A^{'} B^{'}$ 为一边，在给出的图形上用尺规作出 $△ A^{'} B^{'} C^{'}$ ，使得 $△ A^{'} B^{'} {C^{'}}^{'} ∽ △ A B C$ ，不写作法，保留作图痕迹．

(2)、在已有的图形上画出一组对应角平分线，并据此写出已知、求证和证明过程．

查看试题解析
21. 2019年12月以来，湖北省武汉市部分医院陆续发现不明原因肺炎病例，现已证实该肺炎为一种新型冠状病毒感染的肺炎，其传染性较强.为了有效地避免交叉感染，需要采取以下防护措施：①戴口罩；②勤洗手；③少出门；④重隔离；⑤捂口鼻；⑥谨慎吃．某公司为了解员工对防护措施的了解程度（包括不了解、了解很少、基本了解和很了解），通过网上问卷调查的方式进行了随机抽样调查（每名员工必须且只能选择一项），并将调查结果绘制成如下两幅统计图．

请你根据上面的信息，解答下列问题

(1)、本次共调查了名员工，条形统计图中 $m =$ ；

(2)、若该公司共有员工1000名，请你估计不了解防护措施的人数；

(3)、在调查中，发现有4名员工对防护措施很了解，其中有3名男员工、1名女员工.若准备从他们中随机抽取2名，让其在公司群内普及防护措施，求恰好抽中一男一女的概率．

查看试题解析
22. 如图，在矩形 $A B C D$ 中， $∠ B A D$ 的平分线交 $B C$ 于点 $E$ ， $E F ⊥ A D$ 于点 $F$ ， $D G ⊥ A E$ 于点 $G$ ， $D G$ 与 $E F$ 交于点 $O$ ， $A D = A E$ ．

(1)、求证： $A B = A G$ ；

(2)、已知 $A B = 1$ ，求 $O D$ 的长．

查看试题解析
23. “疫情”期间，李晨在家制作一种工艺品，并通过网络平台进行线上销售.经过一段时间后发现：当售价是40元/件时，每天可售出该商品60件，且售价每降低1元，就会多售出3件，设该商品的售价为x元/件（20≤x≤40）.

(1)、请用含售价x（元/件）的代数式表示每天能售出该工艺品的件数；

(2)、已知每件工艺品需要20元成本，每天销售该工艺品的纯利润为900元.
①求该商品的售价；

②为了支持“抗疫”行动，李晨决定每销售一件该工艺品便通过网络平台自动向某救助基金会捐款0.5元，求李晨每天通过销售该工艺品捐款的数额.

查看试题解析
24. 如图所示，在等腰△ABC中，AB＝AC＝10cm，BC＝16cm．点D由点A出发沿AB方向向点B匀速运动，同时点E由点B出发沿BC方向向点C匀速运动，它们的速度均为1cm/s．连接DE，设运动时间为t（s）（0＜t＜10），解答下列问题：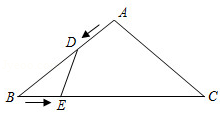

(1)、当t为何值时，△BDE的面积为7.5cm²；

(2)、在点D，E的运动中，是否存在时间t，使得
△BDE与△ABC相似？若存在，请求出对应的时间t；若不存在，请说明理由．

查看试题解析
25. 定义：若关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个实数根 $x_{1}$ ， $x_{2} (x_{1} < x_{2})$ ，分别以 $x_{1}$ ， $x_{2}$ 为横坐标和纵坐标得到点 $M (x_{1} ， x_{2})$ ，则称点 $M$ 为该一元二次方程的衍生点．

(1)、若关于 $x$ 的一元二次方程为 $x^{2} - (2 m - 1) x + m^{2} - m = 0$ ．
①求证：不论 $m$ 为何值，该方程总有两个不相等的实数根，并求出该方程的衍生点 $M$ 的坐标；

②由①得到的衍生点 $M$ 在直线 $l$ ： $y = - x + 3$ 与坐标轴围成的区域上，求 $m$ 的取值范围．

(2)、是否存在 $b$ ， $c$ ，使得不论 $k (k \neq 0)$ 为何值，关于 $x$ 的方程 $x^{2} + b x + c = 0$ 的衍生点 $M$ 始终在直线 $y = k x + 2 (5 - k)$ 的图象？若有，求出 $b$ ， $c$ 的值：若没有，说明理由．

查看试题解析