福建省南平市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-03-02 类型:期中考试
一、单选题
-
1. 下列图形既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知 是关于 的方程 的一个根,则m的值为( )A、2 B、-1 C、3 D、43. 下列图案中,不能由其中一个图形通过旋转而构成的是( )A、
2. 已知 是关于 的方程 的一个根,则m的值为( )A、2 B、-1 C、3 D、43. 下列图案中,不能由其中一个图形通过旋转而构成的是( )A、 B、
B、 C、
C、 D、
D、 4. 将二次函数 的图象向左平移1个单位,则平移后的二次函数的解析式为( )A、 B、 C、 D、5. 二次函数 的图象是( )A、
4. 将二次函数 的图象向左平移1个单位,则平移后的二次函数的解析式为( )A、 B、 C、 D、5. 二次函数 的图象是( )A、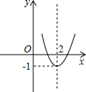 B、
B、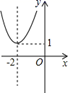 C、
C、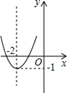 D、
D、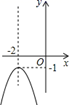 6. 如图,将矩形 绕点 顺时针旋转到矩形 的位置,旋转角为 ( ),若 ,则 的度数为( )
6. 如图,将矩形 绕点 顺时针旋转到矩形 的位置,旋转角为 ( ),若 ,则 的度数为( ) A、 B、 C、 D、7. 如图, 是 的内接三角形, 是 的直径,点 在 上.若 ,则 的度数为( )
A、 B、 C、 D、7. 如图, 是 的内接三角形, 是 的直径,点 在 上.若 ,则 的度数为( )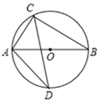 A、 B、 C、 D、8. 已知二次函数y=a(x﹣2)2+c,当x=x1时,函数值为y1;当x=x2时,函数值为y2 , 若|x1﹣2|>|x2﹣2|,则下列表达式正确的是( )A、y1+y2>0 B、y1﹣y2>0 C、a(y1﹣y2)>0 D、a(y1+y2)>09. 如图,在平面直角坐标系中,O是菱形 对角线 的中点, 轴且 , ,将菱形 绕点O旋转,使点D落在x轴上,则旋转后点C的对应点的坐标是( )
A、 B、 C、 D、8. 已知二次函数y=a(x﹣2)2+c,当x=x1时,函数值为y1;当x=x2时,函数值为y2 , 若|x1﹣2|>|x2﹣2|,则下列表达式正确的是( )A、y1+y2>0 B、y1﹣y2>0 C、a(y1﹣y2)>0 D、a(y1+y2)>09. 如图,在平面直角坐标系中,O是菱形 对角线 的中点, 轴且 , ,将菱形 绕点O旋转,使点D落在x轴上,则旋转后点C的对应点的坐标是( ) A、 B、 C、 D、 或10. 如图, 是 上任意一点,点 在 外,已知 , , 是等边三角形,则 的面积的最大值为( )
A、 B、 C、 D、 或10. 如图, 是 上任意一点,点 在 外,已知 , , 是等边三角形,则 的面积的最大值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知点 与点 关于原点对称,则a+b= .12. 方程 的解是.13. 如图,已知 是 的直径,点 , 在 上, , ,则 的半径为 .
 14. 已知点 , 在二次函数 的图象上,则 与 的大小关系为 .(填“ ”“ ”或“ ”)15. 有两个直角三角板,其中 , ,按图①的方式叠放,先将 固定,再将 绕顶点 顺时针旋转,使 (如图②所示),则旋转角 的度数为 .
14. 已知点 , 在二次函数 的图象上,则 与 的大小关系为 .(填“ ”“ ”或“ ”)15. 有两个直角三角板,其中 , ,按图①的方式叠放,先将 固定,再将 绕顶点 顺时针旋转,使 (如图②所示),则旋转角 的度数为 .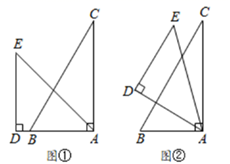 16. 已知函数y=ax2﹣(a﹣1)x﹣2a+1,当0<x<3时,y随x的增大而增大,则a的取值范围是.
16. 已知函数y=ax2﹣(a﹣1)x﹣2a+1,当0<x<3时,y随x的增大而增大,则a的取值范围是.三、解答题
-
17. 解方程: .18. 用配方法把二次函数y=﹣2x2+6x+4化为y=a(x+m)2+k的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.19. 已知关于 的方程 ,求证:不论 取何值,这个方程都有两个实数根.20. 如图是一张长10 dm,宽6 dm矩形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖方盒.
 (1)、无盖方盒盒底的长为dm,宽为dm(用含x的式子表示)(2)、若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.21. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)、无盖方盒盒底的长为dm,宽为dm(用含x的式子表示)(2)、若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.21. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0) (1)、画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;(2)、画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;(3)、在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.22. “绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)、画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;(2)、画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;(3)、在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.22. “绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)、求该型号自行车的进价和标价分别是多少元?
(2)、若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
23. 如图,已知 的直径 弦 于点 ,且 是 的中点,连接 并延长交 于点 . (1)、求证: ;(2)、若 ,求 的长.24. 在△ABC 中,AB=BC=2,∠ABC=120°,将△ABC 绕点 B 顺时针旋转角α(0°<α<90°)得△A1BC1 , A1B 交 AC 于点 E,A1C1 分别交 AC、BC 于 D、F 两点.
(1)、求证: ;(2)、若 ,求 的长.24. 在△ABC 中,AB=BC=2,∠ABC=120°,将△ABC 绕点 B 顺时针旋转角α(0°<α<90°)得△A1BC1 , A1B 交 AC 于点 E,A1C1 分别交 AC、BC 于 D、F 两点. (1)、如图 1,观察并猜想,在旋转过程中,线段 EA1 与 FC 有怎样的数量关系? 并证明你的结论;(2)、如图 2,当α=30°时,试判断四边形 BC1DA 的形状,并说明理由;(3)、在(2)的情况下,求 ED 的长.25. 如图,已知二次函数 的图象交 轴于点 , ,交 轴于点 ,且 ,直线 ( )与二次函数的图象交于点 , (点 在点 的右边),交 轴于点 ,交 轴于点 .
(1)、如图 1,观察并猜想,在旋转过程中,线段 EA1 与 FC 有怎样的数量关系? 并证明你的结论;(2)、如图 2,当α=30°时,试判断四边形 BC1DA 的形状,并说明理由;(3)、在(2)的情况下,求 ED 的长.25. 如图,已知二次函数 的图象交 轴于点 , ,交 轴于点 ,且 ,直线 ( )与二次函数的图象交于点 , (点 在点 的右边),交 轴于点 ,交 轴于点 .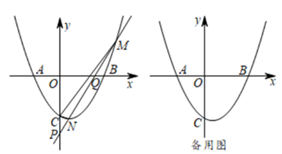 (1)、求二次函数的解析式;(2)、若 , ,求 的面积;(3)、若 ,直线 与 轴相交于点 ,求 的取值范围.
(1)、求二次函数的解析式;(2)、若 , ,求 的面积;(3)、若 ,直线 与 轴相交于点 ,求 的取值范围.