福建省龙岩市长汀县2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-03-02 类型：期中考试

进入出卷网下载

一、单选题

1. 青铜器是一种世界性文明的象征，我国青铜器制作精美，它的纹饰不但蕴含了丰富的文化内涵，大多数图案还具有几何中的对称美．下列纹饰图案中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 由二次函数 $y = 2 {(x - 3)}^{2} + 1$ ，可知（）

A、其图象的开口向下 B、其图象的对称轴为直线x=-3 C、其最小值为1 D、当x<3时，y随x的增大而增大

查看试题解析
3. 以3和4为根的一元二次方程是（）

A、 $x^{2} - 7 x + 12 = 0$ B、 $x^{2} + 7 x + 12 = 0$ C、 $x^{2} + 7 x - 12 = 0$ D、 $x^{2} - 7 x - 12 = 0$

查看试题解析
4. 抛物线y=2（x﹣2）²+5向左平移3个单位长度，再向下平移2个单位长度，此时抛物线的对称轴是（）

A、x=2 B、x=﹣1 C、x=5 D、x=0

查看试题解析
5. 用配方法解一元二次方程x²+4x﹣3=0时，原方程可变形为（）

A、（x+2）²=1 B、（x+2）²=19 C、（x+2）²=13 D、（x+2）²=7

查看试题解析
6. 在某次聚会上，每两人都握了一次手，所有人共握手10次，设有二人参加这次聚会，则列出方程正确的是（）

A、 $x (x - 1) = 10$ B、 $\frac{x (x - 1)}{2} = 10$ C、 $x (x + 1) = 10$ D、 $\frac{x (x + 1)}{2} = 10$

查看试题解析
7. 如图，将△OAB绕点O逆时针旋转80°，得到△OCD.若∠A＝2∠D＝100°，则∠α的度数是（）

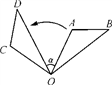A、50° B、60° C、40° D、30°

查看试题解析
8. 将一副三角板顶点重合，三角板ABC绕点A顺时针转动的过程中，∠EAB度数符合下列条件时，三角尺不存在一组边平行的是（三角板边AB＝AE）（）

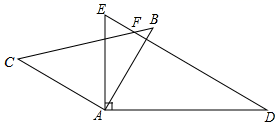A、∠EAB＝30° B、∠EAB＝45° C、∠EAB＝60° D、∠EAB＝75°

查看试题解析
9. 在二次函数y＝x²－2x－3中，当0≤x≤3时，y的最大值和最小值分别是（）

A、0，－4 B、0，－3 C、－3，－4 D、0，0

查看试题解析
10. 已知 $a ， b$ 是非零实数， $| a | > | b |$ ，在同一平面直角坐标系中，二次函数 $y_{1} = a x^{2} + b x$ 与一次函数 $y_{2} = a x + b$ 的大致图象不可能是（）

A、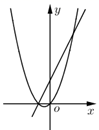 B、 C、 D、

查看试题解析

二、填空题

11. 点P（﹣3，4）关于原点对称的点的坐标是．

查看试题解析
12. 方程（x﹣1）（x+2）=0的解是．

查看试题解析
13. 抛物线 $y = 3 {(x - 1)}^{2} + 8$ 的顶点坐标为．

查看试题解析
14. 若关于x的一元二次方程 $a x^{2} - x - \frac{1}{4} = 0 (a \neq 0)$ 有两个不相等的实数根，则点 $P (a + 1, - a - 3)$ 在第象限．

查看试题解析
15. 某一型号飞机着陆后滑行的距离y（单位：m）与滑行时间x（单位：s）之间的函数关系式是y=60x﹣1.5x² ，该型号飞机着陆后滑行m才能停下来．

查看试题解析
16. 如图，一段抛物线：y=-x(x-3)(0≤x≤3)，记为C₁ ，它与x轴交于两点O ， A₁；将C₁绕A₁旋转180°得到C₂ ，交x轴于A₂；将C₂绕A₂旋转180°得到C₃ ，交x轴于A₃ ，过抛物线C₁ ， C₃顶点的直线与C₁、C₂、C₃围成的如图中的阴影部分，那么该面积为

查看试题解析

三、解答题

17. 用适当的方法解一元二次方程：

(1)、（2x﹣1）²﹣3＝0；

(2)、x（x﹣4）＝1．

查看试题解析
18. 先化简，再求值：（1﹣ $\frac{1}{a}$ ） $\frac{a}{a^{2} - 1}$ ，其中a满足方程a²﹣a﹣2＝0．

查看试题解析
19. 关于x的一元二次方程x²﹣x﹣（m+2）＝0有两个不相等的实数根.

(1)、求m的取值范围；

(2)、若m为符合条件的最小整数，求此方程的根.

查看试题解析
20. 按要求作图，不要求写作法，但要保留作图痕迹．

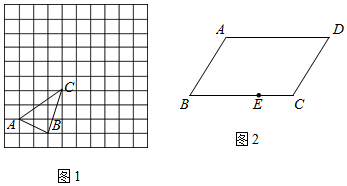(1)、如图1，在10×10的网格中，有一格点三角形ABC．（说明：顶点都在网格线交点处的三角形叫做格点三角形）将△ABC绕点C旋转180°，得到△A'B'C，请直接画出旋转后的△A'B'C．（友情提醒：别忘了标上相应的字母!）

(2)、如图2，四边形ABCD是平行四边形，E为BC上任意一点，请只用直尺（不带刻度）在边AD上找点F，使DF＝BE．

查看试题解析
21. 如图，点M， $N$ 分别在正方形 $A B C D$ 的边 $B C$ ， $C D$ 上，且 $∠ M A N = 45 °$ ，把 $△ A D N$ 绕点A顺时针旋转 $90 °$ 得到 $△ A B E$ .

(1)、求证： $△ A E M$ ≌ $△ A N M$ .

(2)、若 $B M = 3$ ， $D N = 2$ ，求正方形 $A B C D$ 的边长.

查看试题解析
22. 已知 $x = 1 + 2 m, y = 1 - m .$

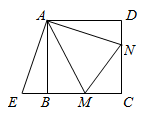(1)、求 $y$ 关于 $x$ 的函数表达式；

(2)、若 $- 3 \leq m \leq 1, x \leq 0,$ 求 $y$ 的取值范围；

(3)、若点 $(x, y)$ 恰好为抛物线 $y = a x^{2} - a x + 1$ 的顶点，求 $a$ 的值.

查看试题解析
23. “五一”期间，恒大影城隆重开业，影城每天运营成本为1000元，试营业期间统计发现，影城每天售出的电影票张数y（张）与电影票售价x（元/张）之间满足一次函数：y=﹣4x+220（10≤x≤50，且x是整数），设影城每天的利润为w（元）（利润=票房收入﹣运营成本）．

(1)、试求w与x之间的函数关系式；

(2)、影城将电影票售价定为多少元/张时，每天获利最大？最大利润是多少元？

查看试题解析
24. 在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合（如图1），其中∠ACB＝∠DFE＝90°，BC＝EF＝3cm，AC＝DF＝4cm，并进行如下研究活动.

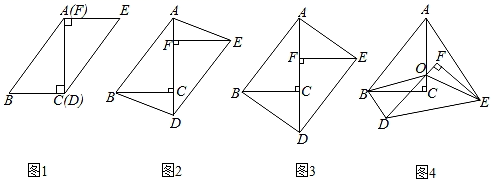(1)、活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD（如图2），当点F与点C重合时停止平移.
（思考）图2中的四边形ABDE是平行四边形吗？请说明理由.

(2)、（发现）当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形（如图3）.求AF的长.

(3)、活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转α度（0≤α≤90），连结OB，OE（如图4）.
（探究）当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由.

查看试题解析
25. 如图，抛物线y＝x²+bx+c与x轴交于点A（﹣1，0）、B两点，与y轴交于点C（0，﹣3）.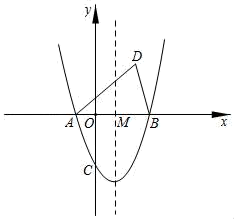

(1)、求抛物线的函数解析式；

(2)、已知点P（m，n）在抛物线上，当﹣2≤m＜3时，直接写n的取值范围；

(3)、抛物线的对称轴与x轴交于点M，点D与点C关于点M对称，试问在该抛物线上是否存在点P，使△ABP与△ABD全等？若存在，请求出所有满足条件的P点的坐标；若不存在，请说明理由.

查看试题解析