福建省福州市闽侯县2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-03-02 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 下列图形中，是中心对称图形的有（   ）

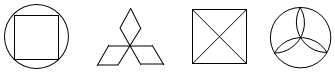    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 2. 下列一元二次方程中，没有实数根的是（    ）
    A、x2＋3x＋2＝0 B、﹣x2＋x＋2＝0 C、（x＋1）2＋2＝0 D、3（x﹣1）2﹣2＝0

    查看试题解析

  • 3. 将二次函数y＝x2＋2x＋3通过配方可化为y＝a（x﹣h）2＋k的形式，结果为（    ）
    A、y＝（x＋1）2＋2 B、y＝（x﹣1）2＋2 C、y＝（x＋1）2﹣2 D、y＝（x﹣1）2﹣2

    查看试题解析

  • 4. 如图，点A，B，C在⊙O上，∠ACB＝38°，则∠AOB等于（    ）

    A、52° B、68° C、76° D、86°

    查看试题解析

  • 5. 对于二次函数y＝（x﹣2）2＋3的图象，下列说法正确的是（    ）
    A、对称轴是x＝﹣2 B、开口向下 C、与x轴有两个交点 D、顶点坐标是(2，3)

    查看试题解析

  • 6. 一件商品的原价是300元，经过两次提价后的价格为363元．如果每次提价的百分率都是x，根据题意，下面列出的方程正确的是（    ）
    A、300（1﹣2x）＝363 B、300（1＋x）＝363 C、300（1﹣x）2＝363 D、300（1＋x）2＝363

    查看试题解析

  • 7. 如图，AB是⊙O的直径，O为圆心，C是⊙O上的点，D是 AC⌢ 上的点，若∠D＝120°，则∠BOC的大小为（    ）

    A、60° B、55° C、58° D、40°

    查看试题解析

  • 8. 矩形ABCD的一条对角线长为5，边AB的长是方程x2﹣6x＋8＝0的一个根，则矩形ABCD的面积为（    ）
    A、12 B、20 C、2 21 D、12或2 21

    查看试题解析

  • 9. 如图，在平面直角坐标系xOy中，△ABC顶点的横、纵坐标都是整数．若将△ABC以某点为旋转中心，旋转得到△A'B'C'，则旋转中心的坐标是（ ）

    A、(1，1) B、(1，﹣1) C、(0，0) D、(1，﹣2)

    查看试题解析

  • 10. 当﹣1＜k＜3时，则直线y＝k与函数y＝ {(x−1)2−1(x≤3)(x−5)2−1(x>3) 交点个数有（    ）
    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题

  • 11. 点P（1，﹣3）关于原点对称的点的坐标是 ．

    查看试题解析

  • 12. 方程x(x﹣1)=0的根是.

    查看试题解析

  • 13. 若二次函数y＝2（x﹣1）2＋1的图象先向左平移2个单位长度，再向下平移2个单位长度，得到函数的解析式为 ．

    查看试题解析

  • 14. 已知△ACB中，∠ACB＝90°，以AB为直径作⊙O，则点C在⊙O（填内、上或外）．

    查看试题解析

  • 15. 已知抛物线y＝（x﹣m）2＋n与x轴交于点(1，0)，(4，0)，则关于x的一元二次方程（x﹣m﹣3）2＋n＝0的解是 ．

    查看试题解析

  • 16. 如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点F在边AC上，并且CF＝1，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是.

    查看试题解析

三、解答题

  • 17. 解方程：x2﹣3x﹣4＝0．

    查看试题解析

  • 18. 已知关于x的一元二次方程x2＋4x＋m﹣2＝0有两个相等的实数根，求m的值及方程的根．

    查看试题解析

  • 19. 已知二次函数y＝0.5x2＋bx＋c中的x，y满足下表：

    x

    …

    ﹣2

    ﹣1

    0

    1

    2

    3

    4

    …

    y

    …

    2.5

    0

    ﹣1.5

    ﹣2

    ﹣1.5

    0

    2.5

    …

    (1)、求这个二次函数的解析式；
    (2)、利用上表，在平面直角坐标系画出这条抛物线；
    (3)、直接写出，当x取何值时，y随x的增大而增大．

    查看试题解析

  • 20. 如图，正方形OABC点A，C分别在x，y轴的正半轴上，将正方形OABC绕点O逆时针旋转30°得正方形OA'B'C'，B'A'与CB相交于点D，连接OD．

    (1)、求证：△OA′D≌△OCD（提示：“HL”）；
    (2)、若OD＝4，求正方形OABC的边长．

    查看试题解析

  • 21. 如图，AB是⊙O的直径，点C在⊙O上，半径OD⊥AC，DE⊥AB于点E，交弦AC于点F，连接BD，AD

    (1)、若∠ABD＝25°，求∠DAC的度数（提示：半径OD⊥AC，可根据垂径定理解题）；
    (2)、求证：DF＝AF．

    查看试题解析

  • 22. 已知：如图，在△ACB中，∠ACB＝90°，AC＝BC，直线 l 经过点A，BD⊥ l 于点D，连接CD．

    (1)、证明A，C，B，D四个点在同一个圆上并画出圆（提示：取AB中点O）；
    (2)、求证：∠ADC＝45°
    (3)、以点C为旋转中心，把△CDB逆时针方向旋转90°，画出旋转后的图形．

    查看试题解析

  • 23. 如图，一段长为45m的篱笆围成一个一边靠墙的矩形花园，墙长为27m，设花园的面积为sm2 ， 平行于墙的边为xm．若x不小于17m，

    (1)、求出s关于x的函数关系式；
    (2)、求s的最大值与最小值．

    查看试题解析

  • 24. 已知如图，⊙O的直径BC＝4 3 ， AB⌢ ＝ AD⌢ ＝ DC⌢ ，点P是射线BD上的一个动点．

    (1)、如图1，求BD的长；
    (2)、如图1，若PB＝8，连接PC，求证PC为⊙O的切线；
    (3)、如图2，连接AP，点P在运动过程中，求AP＋ 12 PB的最小值．

    查看试题解析

  • 25. 已知直线 l ：y1＝x﹣1，抛物线c：y2＝（x﹣h）2＋k．
    (1)、若h＝0，k＝﹣1，求直线 l 与抛物线c的交点坐标；
    (2)、若k＝﹣1时，求当x（可用含h的代数式表示）为何值时，y2＞y1；
    (3)、若k＝h2＋1，设直线 l 与x，y轴与分别交于点A，B，抛物线c的顶点为P，当点A，B，P三点构成的三角形是直角三角形时，请直接写出点P的坐标．

    查看试题解析