福建省福州市罗源县三校2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-03-02 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列四个图案中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知⊙O的半径是3 cm，若圆心O到直线l的距离为1 cm，则⊙O与直线l的位置关系是（）

A、相交 B、相切 C、相离 D、无法确定

查看试题解析
3. 已知关于x的一元二次方程x²+mx﹣8=0的一个实数根为2，则另一实数根及m的值分别为（）

A、4，﹣2 B、﹣4，﹣2 C、4，2 D、﹣4，2

查看试题解析
4. 抛物线y＝－2（x－3）²＋5向左平移4个单位长度，再向下平移3个单位长度后的抛物线顶点坐标是（）

A、（3，5） B、（3，－5） C、（－1，2） D、（－7，2）

查看试题解析
5. 若a＋b＋c＝0，那么二次函数y＝ax²＋bx＋c必过一点是（）

A、（0 ，0） B、（1 ，0） C、（－1 ，0） D、（2 ，0）

查看试题解析
6. 如图，将一把两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D、E，量出半径OC=5cm，弦DE=8cm，则直尺的宽度是（）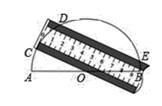

A、4cm B、3cm C、2cm D、1cm

查看试题解析
7. 已知关于x的方程 $\frac{1}{4}$ x²－（m－3）x＋m²＝0有两个不相等的实数根，那么m的最大整数值是（）

A、2 B、1 C、0 D、－1

查看试题解析
8. 在国庆节期间，某微信群规定：群内的每个人都要发一个红包，并保证群内其他人都能抢到且自己不能抢自己发的红包．若此次抢红包活动，群内所有人共收到42个红包，则该群一共有（）

A、6人 B、7人 C、8人 D、9人

查看试题解析
9. 如图，梯形ABCD中，AB∥DC，AB⊥BC，AB=2cm，CD=4cm．以BC上一点O为圆心的圆经过A、D两点，且∠AOD=90°，则圆心O到弦AD的距离是（）

A、 $\sqrt{6}$ cm B、 $\sqrt{10}$ cm C、 $2 \sqrt{3}$ cm D、 $2 \sqrt{5}$ cm

查看试题解析
10. 若二次函数y＝ax²＋bx－1的最小值为－3，则方程|ax²＋bx－1|＝2的不相同实数根的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 函数 $y = 2 x^{2} + 4 x - 5$ 用配方法转化为 $y = a {(x - h)}^{2} + k$ 的形式是．

查看试题解析
12. 如图所示，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转至△ADE处，使点B落在BC延长线上的D点处，则∠CAE=度．

查看试题解析
13. 如图，PA，PB是⊙O是切线，A，B为切点，AC是⊙O的直径，若∠BAC=25°，则∠P=度．

查看试题解析
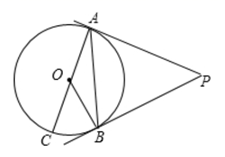14. 如图，点O是△ABC的内切圆的圆心，若∠BAC＝78°，则∠BOC＝度．

查看试题解析
15. 已知二次函数y＝ $\frac{1}{2}$ x²＋2若自变量x的取值范围是－1≤x≤2，则函数y的取值范围是．

查看试题解析
16. 一条抛物线与x轴相交于A，B两点（点A在点B的左侧），若点M，N的坐标分别为（－1，－2），（1，－2），抛物线顶点P在线段MN上移动．点B的横坐标的最大值为3，则点A的横坐标的最小值为．

查看试题解析

三、解答题

17. 解方程：

(1)、3x²－4x－2＝0；

(2)、（x－6）²＝2（6－x）．

查看试题解析
18. 已知抛物线 $y = - x^{2} + bx + c$ 经过点A（3，0），B（﹣1，0）.

(1)、求抛物线的解析式；

(2)、求抛物线的顶点坐标.

查看试题解析
19. 如图，△ABC三个顶点的坐标分别是A（1，1），B（4，2），C（3，4）．

(1)、请画出△ABC关于原点对称的△A₁B₁C₁；通过作图，你发现了△ABC中任意一点（x，y）关于原点中心对称后的点坐标为．

(2)、已知点M坐标为（m，n），点P的坐标为（2，－3），则点M关于点P中心对称的点N的坐标为．

查看试题解析
20. AB是⊙O的一条弦，OD⊥AB，垂足为C，OD交⊙O于点D，点E在⊙O上．

(1)、若∠AOD＝54°，求∠DEB的度数；

(2)、若DC＝2，AB＝8，求⊙O的直径长．

查看试题解析
21. 观察下列一组方程： $① x^{2} - x = 0$ ； $② x^{2} - 3 x + 2 = 0$ ； $③ x^{2} - 5 x + 6 = 0$ ； $④ x^{2} - 7 x + 12 = 0$ ； $\dots$ 它们的根有一定的规律，都是两个连续的自然数，我们称这类一元二次方程为“连根一元二次方程”．

(1)、若 $x^{2} + k x + 56 = 0$ 也是“连根一元二次方程”，写出k的值，并解这个一元二次方程；

(2)、请写出第n个方程和它的根．

查看试题解析
22. 如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD⊥PA，垂足为D．

(1)、求证：CD为⊙O的切线；

(2)、若DC+DA=6，⊙O的直径为10，求AB的长度．

查看试题解析
23.
宏兴企业接到一批产品的生产任务，按要求必须在14天内完成．已知每件产品的出厂价为60元．工人甲第x天生产的产品数量为y件，y与x满足如下关系：y= ${\begin{matrix} 7.5 x (0 \leq x \leq 4) \\ 5 x + 10 (4 < x \leq 14) \end{matrix}$ ．

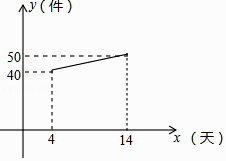(1)、工人甲第几天生产的产品数量为70件？

(2)、设第x天生产的产品成本为P元/件，P与x的函数图象如图．工人甲第x天创造的利润为W元，求W与x的函数关系式，并求出第几天时，利润最大，最大利润是多少？

查看试题解析
24. 已知，点D是等边△ABC内的任一点，连接OA，OB，OC．

(1)、如图1，已知∠AOB＝150°，∠BOC＝120°，将△BOC绕点C按顺时针方向旋转60°得△ADC．
①∠DAO的度数是多少

②用等式表示线段OA，OB，OC之间的数量关系，并证明；

(2)、设∠AOB＝α，∠BOC＝β.
①当α，β满足什么关系时，OA＋OB＋OC有最小值？请在图2中画出符合条件的图形，并说明理由；

②若等边△ABC的边长为1，直接写出OA＋OB＋OC的最小值．

查看试题解析
25. 在平面直角坐标系xOy中，抛物线y＝mx²﹣2mx+n(m≠0)与x轴交于点A ， B ，点A的坐标为(﹣2，0)．

(1)、写出抛物线的对称轴；

(2)、直线 $y = \frac{1}{2} x - 4 m - n$ 过点B ，且与抛物线的另一个交点为C ．
①分别求直线和抛物线所对应的函数表达式；

②点P为抛物线对称轴上的动点，过点P的两条直线l₁：y＝x+a和l₂：y＝﹣x+b组成图形G ．当图形G与线段BC有公共点时，直接写出点P的纵坐标t的取值范围．

查看试题解析