山西省朔州市怀仁市2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-03-02 类型:期中考试
一、单选题
-
1. 下列手机手势解锁图案中,是轴对称图形的是( )A、
 B、
B、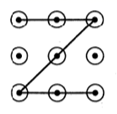 C、
C、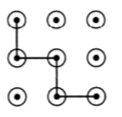 D、
D、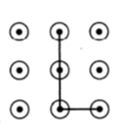 2. 若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )A、2cm B、4cm C、6cm D、8cm3. 平面直角坐标系中的点 与点 关于( )A、原点对称 B、 轴对称 C、 轴对称 D、第一、三象限角平分线对称4. 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
2. 若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )A、2cm B、4cm C、6cm D、8cm3. 平面直角坐标系中的点 与点 关于( )A、原点对称 B、 轴对称 C、 轴对称 D、第一、三象限角平分线对称4. 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( ) A、SAS B、ASA C、AAS D、SSS5. 如图,在△ABC中,已知AB=AC , DE垂直平分AC , ∠A=50°,则∠DCB的度数是( )
A、SAS B、ASA C、AAS D、SSS5. 如图,在△ABC中,已知AB=AC , DE垂直平分AC , ∠A=50°,则∠DCB的度数是( ) A、15° B、30° C、50° D、65°6. 下面说法错误的是( )A、三角形的三条角平分线交于一点 B、三角形的三条中线交于一点 C、三角形的三条高交于一点 D、三角形的三条高所在的直线交于一点7. 一个多边形的内角和是外角和的 倍,则这个多边形的边数为( )A、 B、 C、 D、8. 如图,已知 于点 ,现有四个条件,那么不能得出 的条件是:① ;② ;③ ;④ ( )
A、15° B、30° C、50° D、65°6. 下面说法错误的是( )A、三角形的三条角平分线交于一点 B、三角形的三条中线交于一点 C、三角形的三条高交于一点 D、三角形的三条高所在的直线交于一点7. 一个多边形的内角和是外角和的 倍,则这个多边形的边数为( )A、 B、 C、 D、8. 如图,已知 于点 ,现有四个条件,那么不能得出 的条件是:① ;② ;③ ;④ ( )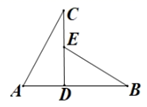 A、①③ B、②③ C、①④ D、②④9. 下列结论中:①有一个外角是 的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的等腰三角形是等边三角形;④三个内角都相等的三角形是等边三角形.其中正确的个数是( )A、4 B、3 C、2 D、110. 如图,四边形 中, ,点 是 的中点,连接 、 , ,给出下列五个结论:① ;② 平分 ;③ ;④ ;⑤ S四边形ABCD , 其中正确的有( )
A、①③ B、②③ C、①④ D、②④9. 下列结论中:①有一个外角是 的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的等腰三角形是等边三角形;④三个内角都相等的三角形是等边三角形.其中正确的个数是( )A、4 B、3 C、2 D、110. 如图,四边形 中, ,点 是 的中点,连接 、 , ,给出下列五个结论:① ;② 平分 ;③ ;④ ;⑤ S四边形ABCD , 其中正确的有( )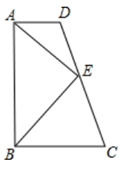 A、3个 B、2个 C、5个 D、4个
A、3个 B、2个 C、5个 D、4个二、填空题
-
11. 如图,在 中, ,点 在 延长线上, 于点 ,交 于点 ,若 , ,则 的长度为 .
 12. 已知 , , 是 的三条边长,化简 的结果为 .13. 如图,∠C=∠D=90º,添加一个条件: (写出一个条件即可),可使 Rt△ABC 与Rt△ABD 全等.
12. 已知 , , 是 的三条边长,化简 的结果为 .13. 如图,∠C=∠D=90º,添加一个条件: (写出一个条件即可),可使 Rt△ABC 与Rt△ABD 全等.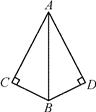 14. 如图,在 中, 、 、 分别是 、 、 的中点,若 的面积是1,则 .
14. 如图,在 中, 、 、 分别是 、 、 的中点,若 的面积是1,则 . 15. 如图,在△ABC中,∠ACB=90º,∠BAC=30º,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有个.
15. 如图,在△ABC中,∠ACB=90º,∠BAC=30º,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有个.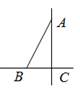
三、解答题
-
16. 在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:

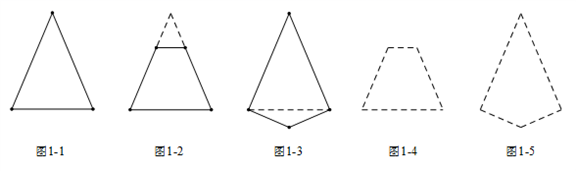 (1)、非等边的等腰三角形有条对称轴,非正方形的长方形有条对称轴,等边三角形有条对称轴;(2)、观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1-2和图1-3都可以看作由图1-1修改得到的,仿照类似的修改方式,请你在图1-4和图1-5中,分别修改图1-2和图1-3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;(3)、小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;(4)、请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.17. 如图,∠C=∠E,AC=AE,点D在BC边上,∠1=∠2,AC和DE相交于点O.求证:△ABC≌△ADE.
(1)、非等边的等腰三角形有条对称轴,非正方形的长方形有条对称轴,等边三角形有条对称轴;(2)、观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1-2和图1-3都可以看作由图1-1修改得到的,仿照类似的修改方式,请你在图1-4和图1-5中,分别修改图1-2和图1-3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;(3)、小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;(4)、请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.17. 如图,∠C=∠E,AC=AE,点D在BC边上,∠1=∠2,AC和DE相交于点O.求证:△ABC≌△ADE.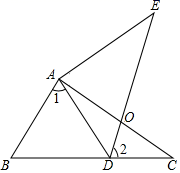 18. 如图,在直角坐标系中,先描出点 ,点 .
18. 如图,在直角坐标系中,先描出点 ,点 . (1)、描出点A关于x轴的对称点 的位置,写出 的坐标;(2)、用尺规在x轴上找一点C,使 的值最小(保留作图痕迹);(3)、用尺规在x轴上找一点P,使 (保留作图痕迹).19. 如图,在△ABC中,∠C=90°,BD平分∠ABC , 交AC于点D , 过点D作DE⊥AB于点E , 点E恰为AB的中点.若DE=1 cm,BD=2 cm,求AC的长.
(1)、描出点A关于x轴的对称点 的位置,写出 的坐标;(2)、用尺规在x轴上找一点C,使 的值最小(保留作图痕迹);(3)、用尺规在x轴上找一点P,使 (保留作图痕迹).19. 如图,在△ABC中,∠C=90°,BD平分∠ABC , 交AC于点D , 过点D作DE⊥AB于点E , 点E恰为AB的中点.若DE=1 cm,BD=2 cm,求AC的长. 20. 如图,在△ABC中, 为 边上的一点, ,求 的度数.
20. 如图,在△ABC中, 为 边上的一点, ,求 的度数.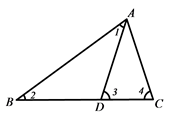 21. 如图,一艘轮船以 海里 小时的速度由南向北航行,在 处测得小岛 在北偏西 的方向上, 小时后,轮船在 处测得小岛 在北偏西 方向上,在小岛 周围 海里内有暗礁,若轮船继续向前航行,有无触礁的危险?
21. 如图,一艘轮船以 海里 小时的速度由南向北航行,在 处测得小岛 在北偏西 的方向上, 小时后,轮船在 处测得小岛 在北偏西 方向上,在小岛 周围 海里内有暗礁,若轮船继续向前航行,有无触礁的危险? 22. 如图, ,点 、 分别在射线 、 上, 是 的平分线, 的反向延长线与 的平分线交于点 .
22. 如图, ,点 、 分别在射线 、 上, 是 的平分线, 的反向延长线与 的平分线交于点 .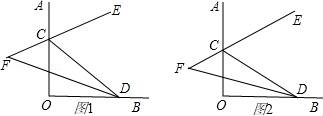 (1)、当 (图1),试求 .(2)、当 、 在射线 、 上任意移动时(不与点 重合)(图2), 的大小是否变化?若变化,请说明理由;若不变化,求出 .23. 如图(1),AB=4cm , AC⊥AB , BD⊥AB , AC=BD=3cm . 点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)、当 (图1),试求 .(2)、当 、 在射线 、 上任意移动时(不与点 重合)(图2), 的大小是否变化?若变化,请说明理由;若不变化,求出 .23. 如图(1),AB=4cm , AC⊥AB , BD⊥AB , AC=BD=3cm . 点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).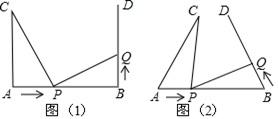 (1)、若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)、如图(2),将图(1)中的“AC⊥AB , BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s , 是否存在实数x , 使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
(1)、若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)、如图(2),将图(1)中的“AC⊥AB , BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s , 是否存在实数x , 使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.