山西省吕梁市兴县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-03-02 类型:期中考试
一、单选题
-
1. 2020年初,新型冠状病毒引发肺炎疫情.一方有难,八方支援,危难时刻,全国多家医院纷纷选派医护人员驰援武汉.下面是四家医院标志的图案部分,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
2. 如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( ) A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF3. 点P(1,﹣2)关于x轴对称的点的坐标为( )A、(1,2) B、(1,﹣2) C、(﹣1,2) D、(﹣1,﹣2)4. 花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配一块与原来大小一样的三角形玻璃,应该带( )
A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF3. 点P(1,﹣2)关于x轴对称的点的坐标为( )A、(1,2) B、(1,﹣2) C、(﹣1,2) D、(﹣1,﹣2)4. 花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配一块与原来大小一样的三角形玻璃,应该带( )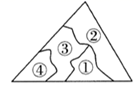 A、第①块 B、第②块 C、第③块 D、第④块5. 如图,点 分别在线段 上, 与 相交于 点, 已知 ,现添加以下的哪个条件仍无法判定 的是( )
A、第①块 B、第②块 C、第③块 D、第④块5. 如图,点 分别在线段 上, 与 相交于 点, 已知 ,现添加以下的哪个条件仍无法判定 的是( )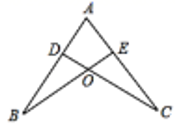 A、 B、 C、 D、6. 如图, 与 关于直线 对称,若 , ,则 度数为( )
A、 B、 C、 D、6. 如图, 与 关于直线 对称,若 , ,则 度数为( )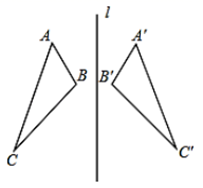 A、 B、 C、 D、7. 三角形的两边长为 和 则第三边长可以为( )A、 B、 C、 D、8. 如图所示,△ABC 中 AB 边上的高线是( )
A、 B、 C、 D、7. 三角形的两边长为 和 则第三边长可以为( )A、 B、 C、 D、8. 如图所示,△ABC 中 AB 边上的高线是( )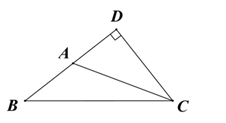 A、线段 DA B、线段 CA C、线段 CD D、线段 BD9. 下列说法中错误的是( )A、三角形的一个外角大于任何一个内角 B、有一个内角是直角的三角形是直角三角形 C、任意三角形的外角和都是 D、三角形的中线、角平分线,高线都是线段10. 小聪同学把一副三角板按如图所示的方式摆放在一起,其中 , , ,则 等于( )
A、线段 DA B、线段 CA C、线段 CD D、线段 BD9. 下列说法中错误的是( )A、三角形的一个外角大于任何一个内角 B、有一个内角是直角的三角形是直角三角形 C、任意三角形的外角和都是 D、三角形的中线、角平分线,高线都是线段10. 小聪同学把一副三角板按如图所示的方式摆放在一起,其中 , , ,则 等于( )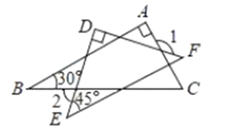 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在门框钉一根木条能固定住门框,不易变形,这里利用的数学原理是 .12. 如图, 中, ,则 .
 13. 一个多边形的外角和是内角和的 ,则这个多边形的边数为 .14. 如图, 为直角三角形, , 于点 ,与 相等的角是 .
13. 一个多边形的外角和是内角和的 ,则这个多边形的边数为 .14. 如图, 为直角三角形, , 于点 ,与 相等的角是 . 15. 一副含有30°和45°的直角三角尺叠放如图,则图中∠α的度数是 .
15. 一副含有30°和45°的直角三角尺叠放如图,则图中∠α的度数是 .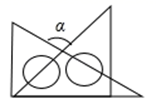
三、解答题
-
16. 如图,在平面直角坐标系 xOy 中, , ,
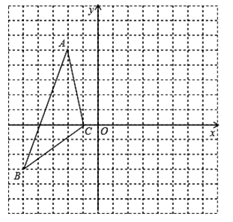 (1)、在图中作出 关于 轴的 对称图形 ;(2)、写出点 , , 的坐标.(3)、求出 的面积.17. 如图,已知点 在线段 上, , , . 试说明: .
(1)、在图中作出 关于 轴的 对称图形 ;(2)、写出点 , , 的坐标.(3)、求出 的面积.17. 如图,已知点 在线段 上, , , . 试说明: .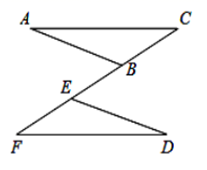
解:因为 (已知)
所以 ▲ ( ▲ )
即 ▲ = ▲
在 和 中
(已知)
(已知)
(已知)
所以 ( ▲ )
18. 如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=48°,∠C=62°,求∠ABE的度数.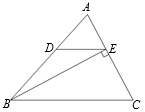 19. 如图,AB = DC,AC = BD,AC、BD交于点E,过E点作EF//BC交CD于F.求证:∠1=∠2.
19. 如图,AB = DC,AC = BD,AC、BD交于点E,过E点作EF//BC交CD于F.求证:∠1=∠2.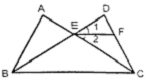 20. 如图, 中,D为BC边上的一点,AD=AC,以线段AD为边作 ,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.
20. 如图, 中,D为BC边上的一点,AD=AC,以线段AD为边作 ,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.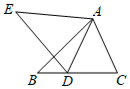 21. 已知:如图,点 在同一条直线上, , , . 求证: .
21. 已知:如图,点 在同一条直线上, , , . 求证: .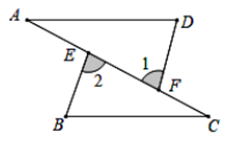 22. 已知 是 的平分线,点 是射线 上一点,点C、D分别在射线 、 上,连接PC、PD .
22. 已知 是 的平分线,点 是射线 上一点,点C、D分别在射线 、 上,连接PC、PD .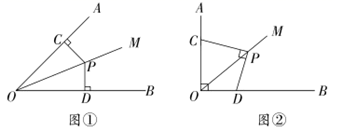 (1)、发现问题
(1)、发现问题如图①,当 , 时,则PC与PD的数量关系是 .
(2)、探究问题如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当 时,PC与PD在(1)中的数量关系还成立吗?说明理由.
23. 探究与发现:(1)、(探究一)我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?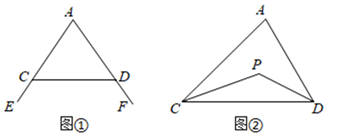
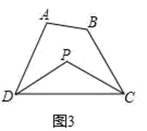
已知:如图①,∠FDC与∠ECD分别为 ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系,并证明你探究的数量关系.
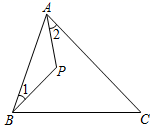
(2)、(探究二)三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?已知:如图②,在 ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠A与∠P的数量关系,并证明你探究的数量关系.
(3)、(探究三)若将 ADC改成任意四边形ABCD呢?已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论直接写出∠A+∠B与∠P的数量关系 .