山西省临汾市襄汾县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-03-02 类型:期中考试
一、单选题
-
1. 下列语句错误的是( )A、无理数都是无限小数 B、 C、有理数和无理数统称实数 D、任何一个正数都有两个平方根2. 下列运算正确的是( )A、 B、 C、 D、3. 如图, ,若 , ,则 长为( )
 A、6 B、5 C、4 D、84. 若 是完全平方式,则m的值是( )A、 B、 C、 或 D、 或5. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、6. 下面是投影屏上出示的抢答题,需要回答符号代表的内容.
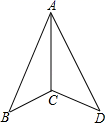
A、6 B、5 C、4 D、84. 若 是完全平方式,则m的值是( )A、 B、 C、 或 D、 或5. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、6. 下面是投影屏上出示的抢答题,需要回答符号代表的内容.如图,已知AB=AD , CB=CD , ∠B=30°,∠BAC=25°,求∠BCD的度数.
解:在ABC和△ADC中,
,
所以△ABC≌△ADC , (@)
所以∠BCA=◎.(全等三角形的★相等)
因为∠B=30°,∠BAC=25°,
所以∠BCA=180°﹣∠B﹣∠BAC=125°,
所以∠BCD=360°﹣2∠BCA=※.
则回答正确的是( )
 A、★代表对应边 B、※代表110° C、@代表ASA D、◎代表∠DAC7. 把 分解因式得 ,则c的值是( )A、3 B、2 C、-3 D、18. 设 ,则( )A、 B、 C、 D、9. 如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到 MBC≌ ABC,所以测得MB的长就是A,B两点间的距离,这里判定 MBC≌ ABC的理由是( )
A、★代表对应边 B、※代表110° C、@代表ASA D、◎代表∠DAC7. 把 分解因式得 ,则c的值是( )A、3 B、2 C、-3 D、18. 设 ,则( )A、 B、 C、 D、9. 如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到 MBC≌ ABC,所以测得MB的长就是A,B两点间的距离,这里判定 MBC≌ ABC的理由是( ) A、SAS B、AAA C、SSS D、ASA10. 如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A、SAS B、AAA C、SSS D、ASA10. 如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )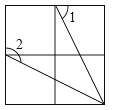 A、150° B、180° C、210° D、225°
A、150° B、180° C、210° D、225°二、填空题
-
11. 计算: .12. 如图, , , 于点 , 于点 , , ,则 的长是 .
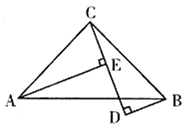 13. 已知 ,则代数式 的值为 .14. 如图,把 绕点 旋转,点 旋转至 边的点 位置, ,则 的度数为 .
13. 已知 ,则代数式 的值为 .14. 如图,把 绕点 旋转,点 旋转至 边的点 位置, ,则 的度数为 . 15. 如图,有 , 两个正方形,现将 放在 的内部得图甲,将 , 并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为5和16,则正方形 , 的面积之和为 .
15. 如图,有 , 两个正方形,现将 放在 的内部得图甲,将 , 并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为5和16,则正方形 , 的面积之和为 .
三、解答题
-
16. 计算(1)、(2)、17. 因式分解(1)、(2)、18. 如图, , , ,
 (1)、求 的度数;(2)、若 ,求证: .19. 先化简,再求值: ,其中20. 已知a﹣b=5,ab=1,求下列各式的值:(1)、(a+b)2;(2)、a3b+ab3 .21. 实践与探索
(1)、求 的度数;(2)、若 ,求证: .19. 先化简,再求值: ,其中20. 已知a﹣b=5,ab=1,求下列各式的值:(1)、(a+b)2;(2)、a3b+ab3 .21. 实践与探索如图1,边长为 的大正方形有一个边长为 的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示)
 (1)、上述操作能验证的等式是__________;(请选择正确的一个)A、 B、 C、(2)、请应用这个公式完成下列各题:
(1)、上述操作能验证的等式是__________;(请选择正确的一个)A、 B、 C、(2)、请应用这个公式完成下列各题:①已知 , ,则 .
②计算:
22. 如图(1),AB⊥BD于点B,ED⊥BD于点D,点C是BD上一点.且BC=DE,CD=AB. (1)、试判断AC与CE的位置关系,并说明理由;(2)、如图(2),若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第(1)问中AC与BE的位置关系还成立吗?(注意字母的变化)23. 长方形的长为 厘米,宽为 厘米,其中 ,如果将原长方形的长和宽各增加3厘米,得到的新长方形面积记为 ,如果将原长方形的长和宽分别减少2厘米,得到的新长方形面积记为 .(1)、若 、 为正整数,请说明: 与 的差一定是5的倍数;(2)、如果 ,求将原长方形的长和宽分别减少7厘米后得到的新长方形面积.
(1)、试判断AC与CE的位置关系,并说明理由;(2)、如图(2),若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第(1)问中AC与BE的位置关系还成立吗?(注意字母的变化)23. 长方形的长为 厘米,宽为 厘米,其中 ,如果将原长方形的长和宽各增加3厘米,得到的新长方形面积记为 ,如果将原长方形的长和宽分别减少2厘米,得到的新长方形面积记为 .(1)、若 、 为正整数,请说明: 与 的差一定是5的倍数;(2)、如果 ,求将原长方形的长和宽分别减少7厘米后得到的新长方形面积.