内蒙古临河四中2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2021-03-02 类型：期中考试

进入出卷网下载

一、单选题

1. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，在五边形 $A B C D E$ 中， $∠ A + ∠ B + ∠ E = 320 °$ ， $D P$ ， $C P$ 分别平分 $∠ E D C$ ， $∠ B C D$ ，则 $∠ P$ 的度数（）

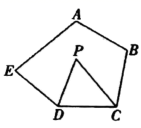A、70° B、65° C、60° D、55°

查看试题解析
3. 已知一个三角形的两条边长分别为4和6，则第三条边的长度不能是（）

A、4 B、7 C、11 D、3

查看试题解析
4. 若一副三角板按如图所示放置，则∠EGA的度数为（）

A、30° B、45° C、60° D、75°

查看试题解析
5. 如图，△ABC≌△AED ，点E在线段BC上，∠1＝40°，则∠AED的度数是（）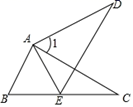

A、70° B、68° C、65° D、60°

查看试题解析
6. 若 $3^{x} = 2$ ， $3^{y} = 5$ ，则 $3^{2 x - y}$ 的值是（）

A、-1 B、 $\frac{1}{3}$ C、20 D、 $\frac{4}{5}$

查看试题解析
7. 如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（）

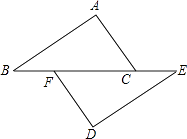A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC

查看试题解析
8. 下列各式中，运算错误的是（）

A、（x+5）（x﹣5）＝x²﹣25 B、（﹣x﹣5）（﹣x+5）＝x²﹣25 C、（x+ $\frac{1}{2}$ ）²＝x²+x+ $\frac{1}{4}$ D、（x﹣3y）²＝x²﹣3xy+9y²

查看试题解析
9. 下面有4道题，小明在横线上面写出了答案：① $(a + b) (b - a) = - a^{2} + b^{2}$ ，② $(- a^{5}) \div {(- a)}^{2} = - a^{3}$ ，③ $3^{2019} \times {(\frac{1}{3})}^{2020} = 3$ ，④若 $a - b = 2$ ，则 $a^{2} - b^{2} - 4 b = 4$ ．他写对答案的题是（）

A、①② B、①②③ C、①②④ D、②③④

查看试题解析
10. 如图， $C$ 为线段 $A E$ 上一动点(不与点 $A$ ， $E$ 重合)，在 $A E$ 同侧分别作等边 $Δ A B C$ 和等边 $Δ C D E$ ， $A D$ 与 $B E$ 交于点 $O$ ， $A D$ 与 $B C$ 交于点 $P$ ， $B E$ 与 $C D$ 交于点 $Q$ ，连接 $P Q$ .下列五个结论：① $A D = B E$ ；② $P Q // A E$ ；③ $A P = B Q$ ；④DE=DP；⑤ $∠ A O B = 60 °$ .其中正确结论的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 多项式 $15 m^{3} n^{2} + 5 m^{2} n - 20 m^{2} n^{3}$ 的公因式是．

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A = 50 °$ ，若剪去 $∠ A$ 得到四边形 $B C D E$ ，则 $∠ 1 + ∠ 2 =$ ．

查看试题解析
13. 若 $x^{2} + 2 (m - 1) x + 9$ 是完全平方式，则 m 的值是．

查看试题解析
14. 一个三角形的三边为2、5、x ，另一个三角形的三边为y、2、6，若这两个三角形全等，则x+y= .

查看试题解析
15. 点（2+a，3）关于y轴对称的点的坐标是（﹣4，2﹣b），则a^b= ．

查看试题解析
16. 如图为6个边长相等的正方形的组合图形，则 $∠ 1 - ∠ 2 + ∠ 3 =$ ．

查看试题解析
17. 如图，在△ABC中，DE是AC的垂直平分线，AE＝3cm ， △ABD的周长为10cm ，那么△ABC的周长为cm ．

查看试题解析
18. 如图，在△ABC中，∠BAC＝90°，AB＝3，AC＝4，BC＝5，EF垂直平分BC，点P为直线EF上的任一点，则AP＋BP的最小值是.

查看试题解析

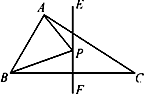
三、解答题

19.

(1)、分解因式 $6 x (a - b) + 4 y (b - a)$ ；

(2)、化解求值
$(3 x - 1) (2 y - 1) + (6 x^{2} y + 4 x y^{2}) \div 2 x y - 1$ ，其中 $x = \frac{1}{2}$ ， $y = - 2$ ；

查看试题解析
20. 如图，点B、F、C、E在直线 $l$ 上（F、C之间不能直接测量），点A、D在 $l$ 异侧，AB∥DE，测得AB=DE，∠A=∠D。

(1)、求证： $△ A B C ≅ △ D E F$ ；

(2)、若BE=10m，BF=3m，求FC的长度。

查看试题解析
21. 如图，已知 $A (- 2 ， 4)$ $B (4 ， 2)$ ， $C (2 ， - 1)$ ，三点.

(1)、作 $Δ A B C$ 关于 $x$ 轴的对称图形 $Δ A_{1} B_{1} C_{1}$ ，写出点 $C$ 关于 $x$ 轴的对称点 $C_{1}$ 的坐标；

(2)、 $P$ 为 $x$ 轴上一点，请在图中找出使 $Δ P A B$ 的周长最小时的点 $P$ 并直接写出此时点 $P$ 的坐标(保留作图痕迹).

查看试题解析
22. 如图，在 $△ A B C$ 中，已知 $A B = A C$ ， $A B$ 的垂直平分线交 $A B$ 于点 $N$ ，交 $A C$ 于点 $M$ ，连接 $M B$ .

(1)、若 $∠ A B C = 70 °$ ，则 $∠ N M A$ 的度数是；

(2)、若 $A B = 8 c m$ ， $△ M B C$ 的周长是 $14 c m$ .
①求 $B C$ 的长度；

②若点 $P$ 为直线 $M N$ 上一点，请你直接写出 $△ P B C$ 周长的最小值.

查看试题解析
23. 如图，△ABC为等边三角形，D、E分别是边AC、BC上的点，且AD＝CE，AE与BD相交于点P.

(1)、求∠BPE的度数；

(2)、若BF⊥AE于点F，试判断BP与PF的数量关系并说明理由.

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C = 2$ ， $∠ B = 40 °$ ，点 $D$ 在线段 $B C$ 上运动（点 $D$ 不与 $B$ ， $C$ 两点重合），连接 $A D$ ，作 $∠ A D E = 40 °$ ， $D E$ 交线段 $A C$ 于点 $E$ ．

(1)、当 $∠ B D A = 115 °$ 时， $∠ B A D =$ （）；点 $D$ 从 $B$ 向 $C$ 运动时， $∠ B D A$ 逐渐变（）（填“大”或“小”）；

(2)、当 $△ A B D ≌ △ D C E$ 时，求 $C D$ 的长；

(3)、在点 $D$ 的运动过程中， $△ A D E$ 的形状也在改变，当 $∠ B D A = 110 °$ 时，请判断 $△ A D E$ 的形状，并证明．

查看试题解析