江西省南昌市2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2021-03-02 类型：期中考试

进入出卷网下载

一、单选题

1. $△ A B C$ 中，已知： $∠ A = 40 °$ ， $∠ B = 45 °$ ，则 $△ A B C$ 中按角分类是（）．

A、锐角三角形 B、直角三角形 C、钝角三角形 D、斜三角形

查看试题解析
2. 斐波那契螺旋线也称为“黄金螺旋线”，它是根据斐波那契数列画出米的螺旋曲线，科学家在自然界中发现存在许多斐波那契螺旋线图案．下列斐波那契螺旋线图案中属于轴对称图形的是（）．

A、 B、 C、 D、

查看试题解析
3. 一个正多边形的每一个内角是 $135 °$ ，则从这个正多边形的一个顶点出发可作（）条对角线．

A、5 B、4 C、3 D、2

查看试题解析
4. 我国的纸伞工艺十分巧妙，如图，伞圈 D 能沿着伞柄滑动，伞不论张开还是缩拢，伞柄 AP 始终平分同一平面内所成的角∠BAC，为了证明这个结论，我们的依据是（）

A、SAS B、SSS C、AAS D、ASA

查看试题解析
5. 已知：AD是 $△ A B C$ 的中线， $A B = 5$ ， $A C = 7$ ，则AD的取值范围是（）．

A、 $5 < A D < 7$ B、 $2 < A D < 10$ C、 $1 < A D < 6$ D、 $2 < A D < 12$

查看试题解析
6. 如图，边长是6的等边 $△ A B C$ ，BD为 $∠ A B C$ 的平分线，动点P ， Q分别在线段BC ， BD上运动，连接CQ ， PQ ，当线段 $C Q + P Q$ 的长度最短时，BP的长度为（）．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. $△ A B C$ 中，已知 $∠ A = 70 °$ ， $∠ B = 60 °$ ，则 $∠ C$ 的外角为度．

查看试题解析
8. 一个多边形的每个外角都是36°，这个多边形是边形

查看试题解析
9. 如图，图中的两个三角形全等，图中的字母表示三角形的边长，则 $∠ 1$ 的度数等于．

查看试题解析
10. 如图，Rt△ABC中，∠B=90°，AB=3cm，BC=4cm，将△ABC折叠，使点C与A重合，得折痕DE，则△ABE的周长等于cm.

查看试题解析
11. 如图，已知： $A B ⊥ C D$ ，且 $A B = C D$ ，E、F是AD上的两点， $C E ⊥ A D$ ， $B F ⊥ A D$ ．若 $C E = 3$ ， $B F = 2$ ， $E F = 1$ ，则 $A D =$

查看试题解析
12. 如图， $△ A B C$ 中． $A C = B C$ ， $∠ A C B = 100 °$ ，点D在线段AB上运动（D不与A、B重合），连接CD ，作 $∠ C D E = 30 °$ ，DE交BC于点E ，若 $△ B D E$ 是等腰三角形，则 $∠ A D C$ 的度数是．

查看试题解析

三、解答题

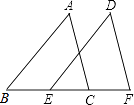
13. 从7根长度都是1的牙签中选取部分或者全部来摆放三角形（牙签不可以折断），你能摆放出多少种形状不同的三角形（两个全等三角形视为一种三角形）？并请你一一写出每种三角形的三边长．

查看试题解析
14. 如图，点B、E、C、F在同一直线上，AB=DE，AC=DF，BE=CF．求证：∠A=∠D．

查看试题解析
15. 如图，在 $△ A B C$ 中，D是BC边上的一点， $A B = D B$ ，BE平分 $∠ A B C$ ，交AC边于点E ，连接DE ．

(1)、求证： $△ A B E ≅ △ D B E$ ；

(2)、若 $∠ C = 50 °$ ， $∠ C D E = 80 °$ ，求 $∠ A E B$ 的度数．

查看试题解析
16. 如图，在平面直角坐标系中，已知 $△ A B C$ 的三个顶点的坐标分别是 $A (- 2 ， 4)$ ， $B (- 4 ， 3)$ ， $C (- 3 ， 1)$ ；

(1)、在图中画出 $△ A B C$ 关于y轴的对称图形 $△ A^{'} B^{'} C^{'}$ ；

(2)、在下面的空格中直接写出点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标：
$A^{'}$ （，）， $B^{'}$ （，）， $C^{'}$ （，）．

查看试题解析
17. 在三角形纸片ABC中， $∠ A B C = 90 °$ ， $∠ A = 30 °$ ， $A C = 4$ ，点E在AC上， $A E = 3$ ．将三角形纸片ABC按图中方式折叠，使点A的对应点 $A^{'}$ 落在AB的延长线上，折痕为ED ， $A^{'} E$ 交BC于点F ．

(1)、求 $∠ C F E$ 的度数；

(2)、求BF的长度．

查看试题解析
18. 如图，在 $△ A B C$ 中，已知： $A B = A D = D C$ ．

(1)、写出图中所有等腰三角形，若 $∠ B A D = 40 °$ ．求 $∠ C$ 的度数：

(2)、若 $∠ B A D = x$ ， $∠ C = y$ ，请用含x的式子表示y ．

查看试题解析
19. 如图， $△ A B C$ 的角平分线AD ， BE相交于点P ， $∠ A P B = 135 °$ ．

(1)、求证： $△ A B C$ 是直角三角形；

(2)、过点P作 $P H ⊥ A D$ 交AC于点H ， PH与BC的延长线相交于点F ．求证： $P A = P F$ ．

查看试题解析
20. 如图，在 $△ A B C$ 中，已知： $A B = 10$ ， $A C = 8$ ，AD是它的角平分线， $D E ⊥ A C$ 且 $D E = 4$ ．

(1)、求 $△ A B C$ 的面积；

(2)、在解完（1）问后，小智经过反思后发现 $\frac{S_{△ A B D}}{S_{△ A C D}} = \frac{A B}{A C}$ ，小慧发现 $\frac{A B}{A C} = \frac{B D}{C D}$ ，请判断小智和小慧的发现是否正确？若正确，请写出证明过程，若错误，请说明理由．

查看试题解析
21. 如图， $△ A B C$ 和 $△ A D E$ 是共顶点A的两个全等的等边三角形．

(1)、该图形显然是轴对称图形．请你仅用无刻度的直尺画出该图形的对称轴l（不必写出作法，但要保留作图痕迹，标注对称轴l）

(2)、在备用图1中，连接BD ， CE ，求证： $B D = C E$ ；

(3)、在备用图2中，连接BE ， CD ，求证： $B E // C D$ ．

查看试题解析