福建省三明市大田县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-03-02 类型:期中考试
一、单选题
-
1. 下列事件是必然事件的是( )A、打开电视机,正在播放动画片 B、2022年世界杯德国队一定能夺得冠军 C、某彩票中奖率是1%,买100张一定会中奖 D、在一只装有5个红球的袋中摸出1球,一定是红球2. 如图,笑脸盖住的点的坐标可能为( )
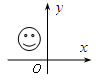 A、(-2,3) B、(3,-4) C、(-4,-6) D、(5,2)3. 如图,已知表示棋子“馬”的坐标分别为(3,2),则表示棋子“車”的点的坐标为( )
A、(-2,3) B、(3,-4) C、(-4,-6) D、(5,2)3. 如图,已知表示棋子“馬”的坐标分别为(3,2),则表示棋子“車”的点的坐标为( )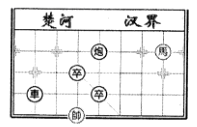 A、(﹣2,1) B、(0,3) C、(﹣3,0) D、(0,﹣3)4. 下列几组数中不能作为直角三角形的三边长的是( )A、9,40,41 B、8,10,12 C、6,8,10 D、7,24,255. 下列四个数中,无理数是( )A、 B、 C、- D、-0.16. 下列计算结果正确的是( )A、 B、 C、 D、7. 如图,AD=1,点M表示的实数是( )
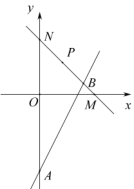
A、(﹣2,1) B、(0,3) C、(﹣3,0) D、(0,﹣3)4. 下列几组数中不能作为直角三角形的三边长的是( )A、9,40,41 B、8,10,12 C、6,8,10 D、7,24,255. 下列四个数中,无理数是( )A、 B、 C、- D、-0.16. 下列计算结果正确的是( )A、 B、 C、 D、7. 如图,AD=1,点M表示的实数是( )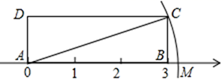 A、 B、 C、3 D、-38. 若 =x﹣3成立,则满足的条件是( )A、x>3 B、x<3 C、x≥3 D、x≤39. A、B两点在一次函数图象上的位置如图所示,两点的坐标分别是 , ,下列结论正确的是( )
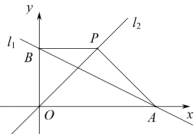
A、 B、 C、3 D、-38. 若 =x﹣3成立,则满足的条件是( )A、x>3 B、x<3 C、x≥3 D、x≤39. A、B两点在一次函数图象上的位置如图所示,两点的坐标分别是 , ,下列结论正确的是( )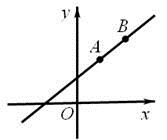 A、 B、 C、 D、10. 图1是我国著名的“赵爽弦图”,它是由四个全等的直角三角形所围成.将四个直角三角形的较短边(如 )向外延长1倍得到点 , , , ,并连结得到图2.已知正方形 与正方形 的面积分别为 和 ,则图2中阴影部分的面积是( )
A、 B、 C、 D、10. 图1是我国著名的“赵爽弦图”,它是由四个全等的直角三角形所围成.将四个直角三角形的较短边(如 )向外延长1倍得到点 , , , ,并连结得到图2.已知正方形 与正方形 的面积分别为 和 ,则图2中阴影部分的面积是( )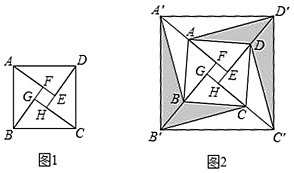 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 当x=时,点M(x -3,x -1)在y轴上.12. 某同学遇到一道不会做的选择题,在四个选项中有且只有一个是正确的,则他选对的概率是 .
13. 点 与点B关于x轴对称,则B点的坐标14. 最简二次根式 与 可以合并,则m= .15. 如图7,正方形①,②的一边在同一直线上,正方形③的一个顶点也在该直线上,且有两个顶点分别与正方形①,②的两个顶点重合,若正方形①,②的面积分别3cm2和4cm2 , 则正方形③的面积为cm2 .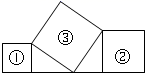 16. 如图,点M , N把线段 分割成 , 和 ,若以 , , 为边的三角形是一个直角三角形,则称点M , N是线段 的“勾股分割点”已知点M , N是线段 的“勾股分割点”,若 , ,则 的长为 .
16. 如图,点M , N把线段 分割成 , 和 ,若以 , , 为边的三角形是一个直角三角形,则称点M , N是线段 的“勾股分割点”已知点M , N是线段 的“勾股分割点”,若 , ,则 的长为 .
三、解答题
-
17. 求下列各式中的x的值.(1)、(2)、18. 计算:(1)、(2)、19. 在一个不透明的袋中装有2个黄球,3个黑球和7个红球,它们除颜色外其他都相同.(1)、将袋中的球摇均匀后,求从袋中随机摸出一个球是黄球的概率;(2)、如果将若干个红球涂成其他颜色,使从袋中随机摸出一个球是红球的概率是 ,请问要将多少个红球涂成其他颜色.20. 如图,在平面直角坐标系 中, , , .
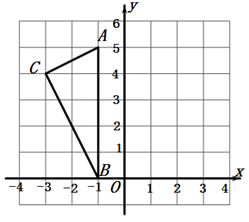 (1)、在图中作出 关于y轴的对称图形 ;(2)、写出点 , , 的坐标;(3)、判断 的形状,并说明理由.21. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的图象如图所示:
(1)、在图中作出 关于y轴的对称图形 ;(2)、写出点 , , 的坐标;(3)、判断 的形状,并说明理由.21. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的图象如图所示: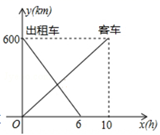 (1)、客车的速度是千米/小时,出租车的速度是千米小时;(2)、求两车相遇的时间.22. 如图是一直角三角形纸片,两直角边AC=6,BC=8,现将直角三角形沿直线AD折叠,使AC边落在斜边AB上,且与AE重合.
(1)、客车的速度是千米/小时,出租车的速度是千米小时;(2)、求两车相遇的时间.22. 如图是一直角三角形纸片,两直角边AC=6,BC=8,现将直角三角形沿直线AD折叠,使AC边落在斜边AB上,且与AE重合.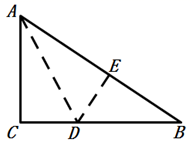 (1)、求EB长;(2)、求△DBE的面积.23. 先阅读下列解答过程,然后再解答:小芳同学在研究化简 中发现:首先把 化为 ﹐由于 , ,即: , ,所以 ,
(1)、求EB长;(2)、求△DBE的面积.23. 先阅读下列解答过程,然后再解答:小芳同学在研究化简 中发现:首先把 化为 ﹐由于 , ,即: , ,所以 ,问题:
(1)、填空: , ﹔(2)、进一步研究发现:形如 的化简,只要我们找到两个正数a , b( ),使 , ,即 , ﹐那么便有: .(3)、化简: (请写出化简过程)