福建省泉州市惠安县第一联盟2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-03-02 类型:期中考试
一、单选题
-
1. 在实数﹣ ,0, ,π,中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 下列运算结果正确的是( )A、 B、 C、 D、3. 的算术平方根是( )
A、 B、 C、± D、4. 下列计算正确的是( )A、 B、 C、 D、5. 将多项式 变为 的形式,结果正确的是( )A、 B、 C、 D、6. 已知 则 的大小关系是( )A、 B、 C、 D、7. 计算 结果正确的是( )A、1 B、 C、 D、-18. 如图,已知 ,那么添加下列一个条件后,仍无法判定 的是( )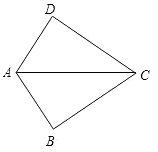 A、 B、 C、 D、9. 如图, ,且 . 、 是 上两点, , .若 , , ,则 的长为( )
A、 B、 C、 D、9. 如图, ,且 . 、 是 上两点, , .若 , , ,则 的长为( )
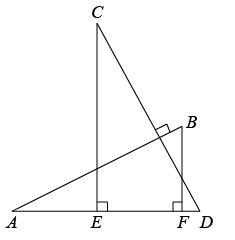 A、 B、 C、 D、10. 设681×2019﹣681×2018=a , 2015×2016﹣2013×2018=b , ,则a , b , c的大小关系是( )A、b<c<a B、a<c<b C、b<a<c D、c<b<a
A、 B、 C、 D、10. 设681×2019﹣681×2018=a , 2015×2016﹣2013×2018=b , ,则a , b , c的大小关系是( )A、b<c<a B、a<c<b C、b<a<c D、c<b<a二、填空题
-
11. 比较大小: 3(填“>”、“<”或“=”号)12. 若am=3,an=4,则am+n=.13. 若多项式与单项式 的积是 ,则该多项式为 .14. 关于 的多项式 展开后不含 的一次项,则 .15. 若 ,则 的值为 .16. 如图, , , , ,则四边形 与 面积的比值是 .

三、解答题
-
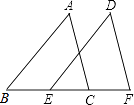
17. 计算:18. 计算:(1)、(2)、19. 因式分解:(1)、(2)、20. 先化简,再求值: ,其中 .21. 如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
 22. 图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
22. 图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.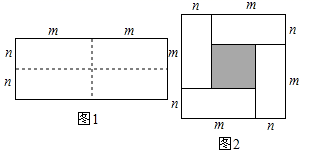 (1)、请用两种不同的方法求图2中阴影部分的面积 直接用含m , n的代数式表示
(1)、请用两种不同的方法求图2中阴影部分的面积 直接用含m , n的代数式表示方法1:
方法2:
(2)、根据(1)中结论,请你写出下列三个代数式之间的一个等量关系: ;代数式: , ,mn(3)、根据(2)题中的等量关系,解决如下问题:已知 , ,求a-b和 的值.23. 双十一购物节即将到来,某商场设计了两种的促销方案,并有以下两种销售量预期.预期一:第1步,销售量扩大为原来的a倍.第2步,再扩大为第1步销售量的b倍.预期二:第1步,销售量扩大为原来的 倍;第2步,再扩大为第1步销售量的 倍;其中a , b为不相等的正数,请问两种预期中,哪种销售量更多?试说明理由.

