福建省南平市2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-03-02 类型:期中考试
一、单选题
-
1. 下列图案是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 已知△ABC≌△DEF,∠A=80°,∠E=40°,则∠F等于( )A、80° B、40° C、60° D、120°3. 点P(﹣1,2)关于y轴对称的点的坐标是( )A、(1,2) B、(﹣1,2) C、(1,﹣2) D、(﹣1,﹣2)4. 到三角形的三边距离相等的点是( )A、三条高的交点 B、三条中线的交点 C、三条角平分线的交点 D、不能确定5. 一个三角形的两边长分别为3和8,第三边长是一个偶数,则第三边的长不能为( )A、6 B、8 C、10 D、126. 如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( )A、4 B、5 C、6 D、77. 如图, 是 的角平分线, ,则 与 的面积比为( ).
2. 已知△ABC≌△DEF,∠A=80°,∠E=40°,则∠F等于( )A、80° B、40° C、60° D、120°3. 点P(﹣1,2)关于y轴对称的点的坐标是( )A、(1,2) B、(﹣1,2) C、(1,﹣2) D、(﹣1,﹣2)4. 到三角形的三边距离相等的点是( )A、三条高的交点 B、三条中线的交点 C、三条角平分线的交点 D、不能确定5. 一个三角形的两边长分别为3和8,第三边长是一个偶数,则第三边的长不能为( )A、6 B、8 C、10 D、126. 如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( )A、4 B、5 C、6 D、77. 如图, 是 的角平分线, ,则 与 的面积比为( ). A、 B、 C、 D、8. 如图,在 中, , 的平分线交 于点 ,且 所在直线是 的垂直平分线,垂足为 .若 ,则 的长为( ).
A、 B、 C、 D、8. 如图,在 中, , 的平分线交 于点 ,且 所在直线是 的垂直平分线,垂足为 .若 ,则 的长为( ).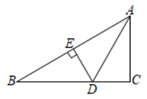 A、6 B、7 C、8 D、99. 如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在△ABC外的点C′处,若∠1=20°,则∠2的度数为( )
A、6 B、7 C、8 D、99. 如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在△ABC外的点C′处,若∠1=20°,则∠2的度数为( ) A、80° B、90° C、100° D、110°10. 如图,在边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接CE,将线段CE绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是( )
A、80° B、90° C、100° D、110°10. 如图,在边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接CE,将线段CE绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是( ) A、6 B、3 C、2 D、1.5
A、6 B、3 C、2 D、1.5二、填空题
-
11. 一个正多边形的每个内角都等于140°,则它是正边形.12. 一个等腰三角形的一个底角为80°,则它的顶用的度数为 .13. 如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,那么 的度数为°.
 14. 如图,已知 , ,则 .
14. 如图,已知 , ,则 . 15. 如图,在 中,点 是 上一动点, , 的垂直平分线分别交 , 于点 , ,在点 的运动过程中, 与 的大小关系是 (填“>”“=”或“<”).
15. 如图,在 中,点 是 上一动点, , 的垂直平分线分别交 , 于点 , ,在点 的运动过程中, 与 的大小关系是 (填“>”“=”或“<”). 16. 如图:等腰三角形 的底边 的长是 ,面积是 ,腰 的垂直平分线 交 于点 ,若 是 边的中点, 为线段 上的动点,则 的最小周长为 .
16. 如图:等腰三角形 的底边 的长是 ,面积是 ,腰 的垂直平分线 交 于点 ,若 是 边的中点, 为线段 上的动点,则 的最小周长为 .
三、解答题
-
17. 如图,AB=AD , ∠B=∠D , ∠BAD=∠CAE , 求证:BC=DE .
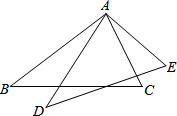 18. 如图,已知 .
18. 如图,已知 .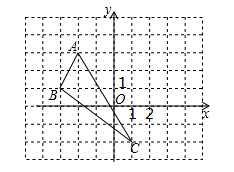 (1)、请画出 关于 轴对称的 (其中 , , 分别是 , , 的对应点,不写画法);(2)、直接写出 , , 三点的坐标: ( , ), ( , ), ( , ).19. 如图,在 中, , 于点 , 于点 ,交 于点 .求证: ≌ .
(1)、请画出 关于 轴对称的 (其中 , , 分别是 , , 的对应点,不写画法);(2)、直接写出 , , 三点的坐标: ( , ), ( , ), ( , ).19. 如图,在 中, , 于点 , 于点 ,交 于点 .求证: ≌ . 20. 如图,AD是△ABC的角平分线,DE⊥AB , DF⊥AC , 垂足分别为E , F , 连接EF , EF与AD相交于点G , 求证:AD是EF的垂直平分线。
20. 如图,AD是△ABC的角平分线,DE⊥AB , DF⊥AC , 垂足分别为E , F , 连接EF , EF与AD相交于点G , 求证:AD是EF的垂直平分线。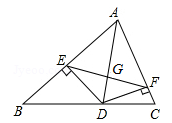 21. 如图,在 中, , .
21. 如图,在 中, , .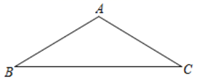 (1)、作 的垂直平分线,分别交 , 于点 , .(尺规作图,保留作图痕迹,不写作法)(2)、在(1)中尺规作图的基础上,连接 ,若 ,求 的长.22. 如图,在 中,边 的垂直平分线 交 于点 ,边 的垂直平分线 交 于点 , 与 相交于点 ,连接 , , 的周长为12cm.
(1)、作 的垂直平分线,分别交 , 于点 , .(尺规作图,保留作图痕迹,不写作法)(2)、在(1)中尺规作图的基础上,连接 ,若 ,求 的长.22. 如图,在 中,边 的垂直平分线 交 于点 ,边 的垂直平分线 交 于点 , 与 相交于点 ,连接 , , 的周长为12cm.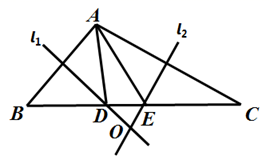 (1)、求 的长;(2)、分别连接 , , ,若 的长为 ,求 的周长.23. 如图,在△ABC中,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)、求 的长;(2)、分别连接 , , ,若 的长为 ,求 的周长.23. 如图,在△ABC中,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F. (1)、求证:∠EFA=90°﹣ ∠B;(2)、若∠B=60°,求证:EF=DF.24. 如图,点 , 分别是等边三角形 的边 , 上的动点(端点除外),点 , 以相同的速度,同时从点 , 出发.
(1)、求证:∠EFA=90°﹣ ∠B;(2)、若∠B=60°,求证:EF=DF.24. 如图,点 , 分别是等边三角形 的边 , 上的动点(端点除外),点 , 以相同的速度,同时从点 , 出发. (1)、如图1,连接 , , .求证: ≌ ;(2)、如图1,当点 , 分别在 , 边上运动时,设 与 相交于点 ,则 的大小是否发生变化?若变化,请说明理由;若不变,求出它的度数;(3)、如图2,当点 , 分别在 , 的延长线上运动时,直线 与 的延长线相交于点 , 的大小是否发生变化?若变化,请说明理由;若不变,求出它的度数.25. 如图,在 中, , , 是边 的中点,以 为边作等边三角形 ,且 与 在直线 的异侧,连接 交 的延长线于点 ,连接 交 于点 .
(1)、如图1,连接 , , .求证: ≌ ;(2)、如图1,当点 , 分别在 , 边上运动时,设 与 相交于点 ,则 的大小是否发生变化?若变化,请说明理由;若不变,求出它的度数;(3)、如图2,当点 , 分别在 , 的延长线上运动时,直线 与 的延长线相交于点 , 的大小是否发生变化?若变化,请说明理由;若不变,求出它的度数.25. 如图,在 中, , , 是边 的中点,以 为边作等边三角形 ,且 与 在直线 的异侧,连接 交 的延长线于点 ,连接 交 于点 . (1)、求证: ;(2)、求证: ;(3)、若 , ,求 的长.
(1)、求证: ;(2)、求证: ;(3)、若 , ,求 的长.