福建省龙岩市长汀县2020-2021学年八年级上学期数学期中试卷
试卷更新日期：2021-03-02 类型：期中考试
一、单选题
-
1. 下列图形中，是轴对称图形的是（ ）A、
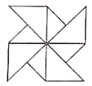B、
C、
D、
2. 如图，两个三角形是全等三角形，x的值是（ ）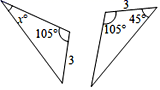
A、30° B、45° C、50° D、85°3. 下列长度的三条线段不能组成三角形的是（ ）A、3、4、5 B、4、4、4 C、4、5、6 D、5、5、104. 已知△ABC中，∠B是∠A的2倍，∠C比∠A大20°，则∠A等于( )A、40° B、60° C、80° D、90°5. 如图所示，小明书上的三角形被墨水污染了，他根据所学知识画出了完全一样的一个三角形，他根据的定理是（ ）
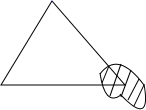A、SSS B、SAS C、AAS D、ASA6. 等腰三角形的一个底角是40°，则它的顶角是（ ）A、100° B、40°或70° C、70° D、40°7. 一幅三角板，如图所示叠放在一起，则图中∠ 的度数是（ ）
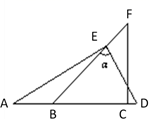A、75° B、60° C、65° D、55°8. 如图，已知△ABC中，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）
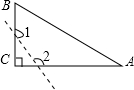A、90° B、135° C、270° D、315°9. 如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC，且∠ADC=110°，则∠MAB=（ ）
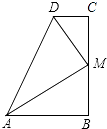A、30° B、35° C、45° D、60°10. 如图， B是直线l上 的一点，线段 AB与L的夹角为a ( 0<a< 180 )，点C在l上，若以 A 、 B 、C 为顶点的三角形是等腰三角形，则满足条件的点C 共有（ ）
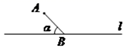A、2 个 B、3 个 C、2 个或 4 个 D、3 个或 4 个二、填空题
-
11. 在平面直角坐标系中，点P(﹣5，3)关于y轴的对称点的坐标为 ．12. 若正多边形的一个内角等于 ，则这个多边形的边数是 ．13. 如图，已知图中的两个三角形全等，则∠α度数是°.
14. 如图，已知∠A＝∠D，要使 ABC与 DCB全等．需添加的条件是（只写一个）．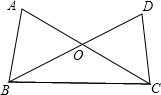
15. 如图，在△ABC中，点D、E、F分别是BC，AB，AC上的点，若∠B=∠C，BF=CD，BD=CE，∠EDF=54°，则∠A=.
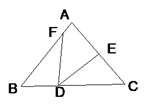16. 如图，在等腰△ABC中，AB＝AC，∠BAC＝50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是 ．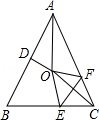
三、解答题
-
17. 如图，已知：AD是△ABC的角平分线，CE是△ABC的高，∠BAC＝60°，∠BCE＝40°，求∠ADB的度数.
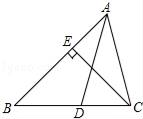18. 如图，EF=BC，DF=AC，DA=EB．求证：∠F=∠C．
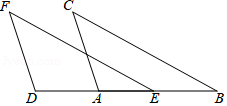19. 如图，在平面直角坐标系 xOy 中，△ABC 的三个顶点的坐标分别是 A(2，3)，B(1，0)，C(1，2).
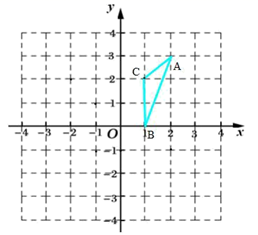(1)、在图中画出△ABC 关于 y 轴对称的(2)、直接写出 三点的坐标：()， ()， ()；
(3)、如果要使以 B、C、D 为顶点的三角形与△ABC 全等，直接写出所有符合条件的点 D 坐标.20. 如图，在 中， .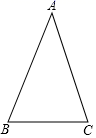
(1)、尺规作图：作 ， 点在 边上.（要求：不写作法，保留作图痕迹）(2)、若 ，求 的度数．21. 如图，在△ABC中，AD平分∠BAC ， 在AB上截取AE＝AC ， 连结DE ， 已知DE＝3.5cm ， BD＝4.5cm ．
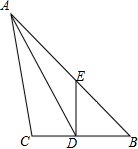(1)、说明△AED≌△ACD的理由；(2)、求线段BC的长．22. 如图，△ABC，△ADE是等边三角形，B，C，D在同一直线上．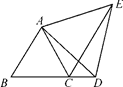
求证：
(1)、CE＝AC＋CD；(2)、∠ECD＝60°.23. 在等边△ABC中，点D在BC边上，点E在AC的延长线上，DE=DA（如图1）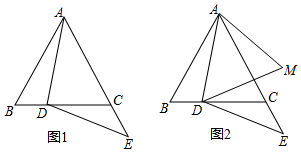
(1)、求证：∠BAD=∠EDC；(2)、如图2，点E关于直线BC的对称点为M，连接DM，AM．小明通过观察，实验提出猜想：在点D运动的过程中，始终有DA=AM，小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的两种想法：
想法1：要证明DA=AM，只需证△ADM是等边三角形；
想法2：连接CM，只需证明△ABD≌△ACM即可．
请你参考上面的想法，帮助小明证明DA=AM（选一种方法即可）
24. 如图，Rt△ABC中，∠ACB=90°，AC=BC ， 点D在斜边AB上，且AD=AC ， 过点B作BE⊥CD交直线CD于点E ．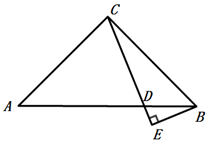
(1)、求∠BCD的度数；(2)、求证：CD=2BE ．25. 如图，在等腰△ABC中，AB＝AC＝3cm ， ∠B＝30°，点D在BC边上由C向B匀速运动（D不与B、C重合），匀速运动速度为1cm/s ， 连接AD ， 作∠ADE＝30°，DE交线段AC于点E ．
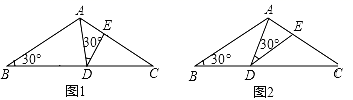(1)、在此运动过程中，∠BDA逐渐变（填“大”或“小”）；D点运动到图1位置时，∠BDA＝75°，则∠BAD＝ ．(2)、点D运动3s后到达图2位置，则CD＝ ． 此时△ABD和△DCE是否全等，请说明理由；(3)、在点D运动过程中，△ADE的形状也在变化，判断当△ADE是等腰三角形时，∠BDA等于多少度（请直接写出结果）