陕西省宝鸡市金台区2020-2021学年高一上学期数学期末考试试卷

试卷更新日期：2021-03-01 类型：期末考试

进入出卷网下载

一、单选题

1. 若点A是点 $B (1, 2, 3)$ 关于x轴对称的点，点C是点 $D (2, - 2, 5)$ 关于y轴对称的点，则 $| A C |$ 等于（）

A、5 B、 $\sqrt{13}$ C、10 D、 $\sqrt{10}$

查看试题解析
2. 将长方体截去一个四棱锥，得到的几何体如右图所示，则该几何体的左视图为（）

A、 B、 C、 D、

查看试题解析
3. 到直线3x－4y＋1＝0的距离为3，且与此直线平行的直线方程是（）

A、3x－4y＋4＝0 B、3x－4y＋4＝0或3x－4y－2＝0 C、3x－4y＋16＝0 D、3x－4y＋16＝0或3x－4y－14＝0

查看试题解析
4. 平面α与平面β平行的条件可以是（　　）

A、α内有无穷多条直线与β平行 B、直线a∥α，a∥β C、直线a⊂α，直线b⊂β，且a∥β，b∥α D、α内的任何直线都与β平行

查看试题解析
5. 已知过点 $A (- 2, m)$ 和点 $B (m, 4)$ 的直线为 $l_{1}$ ， $l_{2} : 2 x + y - 1 = 0$ ， $l_{3} : x + n y + 1 = 0$ ．若 $l_{1} / / l_{2}$ ， $l_{2} ⊥ l_{3}$ ，则 $m + n$ 的值为（）

A、-10 B、-2 C、0 D、8

查看试题解析
6. 已知 $α$ 、 $β$ 是平面， $m$ 、 $n$ 是直线，下列命题中不正确的是（）

A、若 $m // α$ ， $α \cap β = n$ ，则 $m / / n$ B、若 $m / / n$ ， $m ⊥ α$ ，则 $n ⊥ α$ C、若 $m ⊥ α$ ， $m ⊥ β$ ，则 $α // β$ D、若 $m ⊥ α$ ， $m \subset β$ ，则 $α ⊥ β$

查看试题解析
7. 已知 $a ， b$ 是异面直线，直线 $c$ 平行于直线 $a$ ，那么 $c$ 与 $b$ （）

A、一定是异面直线 B、一定是相交直线 C、不可能是平行直线 D、不可能是相交直线

查看试题解析
8. 如图，正方形 $O^{'} A^{'} B^{'} C^{'}$ 的边长为1cm，它是水平放置的一个平面图形用斜二测画法得到的直观图，则原图形的周长是（）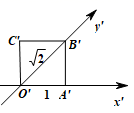

A、8cm B、6cm C、 $2 (1 + \sqrt{3}) cm$ D、 $2 (1 + \sqrt{2}) cm$

查看试题解析
9. 若过点（2，1）的圆与两坐标轴都相切，则圆心到直线 $2 x - y - 3 = 0$ 的距离为（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{3 \sqrt{5}}{5}$ D、 $\frac{4 \sqrt{5}}{5}$

查看试题解析
10. 如图，三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧棱 $A A_{1} ⊥$ 底面 $A_{1} B_{1} C_{1}$ ，底面三角形 $A_{1} B_{1} C_{1}$ 是正三角形，E是BC中点，则下列叙述正确的是（）

A、 $C C_{1}$ 与 $B_{1} E$ 是异面直线 B、 $A C ⊥$ 平面 $A B B_{1} A_{1}$ C、AE， $B_{1} C_{1}$ 为异面直线，且 $A E ⊥ B_{1} C_{1}$ D、 $A_{1} C_{1} / /$ 平面 $A B_{1} E$

查看试题解析
11. 若直线 $l$ ： $y = k x - \sqrt{3}$ 与直线 $2 x +3 y - 6 = 0$ 的交点位于第一象限，则直线的倾斜角的取值范围是（）

A、 $[\frac{π}{6}, \frac{π}{3})$ B、 $[\frac{π}{6}, \frac{π}{2}]$ C、 $(\frac{π}{3}, \frac{π}{2})$ D、 $(\frac{π}{6}, \frac{π}{2})$

查看试题解析
12. 已知 $P (a, b)$ 为圆C: $x^{2} + y^{2} - 2 x - 4 y + 4 = 0$ 上任意一点，则 $\frac{b - 1}{a + 1}$ 的最大值为（）

A、2 B、 $- \frac{4}{3}$ C、 $\frac{4}{3}$ D、0

查看试题解析

二、填空题

13. 当a为任意实数时，直线ax－y＋1－3a＝0恒过定点．

查看试题解析
14. 长方体的长，宽，高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为.

查看试题解析
15. 一块正方形薄铁片的边长为4cm，以它的一个顶点为圆心，边长为半径画弧，沿弧剪下一个扇形（如图）.用这块扇形铁片围成一个圆锥筒，则这个圆锥筒的容积等于 ${cm}^{3}$ .

查看试题解析
16. 两圆相交于两点 $(1, 3)$ 和 $(m, - 1)$ ，两圆圆心都在直线 $x - y + c = 0$ 上，且 $m$ 、 $c$ 均为实数，则 $m + c =$ ．

查看试题解析

三、解答题

17. 已知圆 $C$ 过点 $(0, 1)$ ，半径为 $\sqrt{2}$ ，且圆 $C$ 关于直线 $x + y - 1 = 0$ 对称，圆心在第二象限．

(1)、求圆 $C$ 的方程.

(2)、已知不过原点的直线 $l$ 与圆 $C$ 相切，且在 $x$ 轴、 $y$ 轴上的截距相等，求直线 $l$ 的方程.

查看试题解析
18. 如图， $△ A B C$ 中， $A C = B C = \frac{\sqrt{2}}{2} A B$ ， $A B E D$ 是边长为 $1$ 的正方形，平面 $A B E D$ ⊥平面 $A B C$ ，若 $G$ 、 $F$ 分别是 $E C$ 、 $B D$ 的中点．

(1)、求证： $G F //$ 平面 $A B C$ ；

(2)、求证： $A C$ ⊥平面 $E B C$ ．

查看试题解析
19. 如图，在三棱锥 $P - A B C$ 中， $PA ⊥ AB$ ， $PA ⊥ BC$ ， $AB ⊥ B C$ ， $PA = AB = BC = 2$ ， $D$ 为线段 $A C$ 的中点， $E$ 为线段 $P C$ 上一点．

(1)、求证：平面 $B D E ⊥$ 平面 $P A C$ ；

(2)、当 $P A / /$ 面 $B D E$ 时，求三棱锥 $E - B C D$ 的体积．

查看试题解析
20. 已知点 $A (0, 5)$ ，圆 $C$ ： $x^{2} + y^{2} + 4 x - 12 y + 24 = 0$ .

(1)、若直线 $l$ 过 $A (0, 5)$ 且被圆 $C$ 截得的弦长为 $4 \sqrt{3}$ ，求直线 $l$ 的方程；

(2)、点 $M (- 1, 0)$ ， $N (0, 1)$ ，点 $Q$ 是圆 $C$ 上的任一点，求 $Q$ 点到直线 $M N$ 的距离的最小值．

查看试题解析