初中数学北师大版九年级下学期 第三章 单元测试卷
试卷更新日期:2021-02-25 类型:单元试卷
一、单选题
-
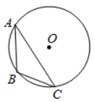
1. 下列说法,正确的是( )A、等弦所对的圆周角相等 B、弦所对的两条弧的中点的连线垂直平分弦,且过圆心 C、切线垂直于圆的半径 D、平分弦的直径垂直于弦2. 已知⊙O的半径为5,圆心O到直线AB的距离为6,则直线AB于⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法确定3. 下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.正确的说法有( )A、1个 B、2个 C、3个 D、4个4. 已知正六角形的边心距为 ,则它的周长是( )A、6 B、12 C、6 D、125. 如图, 是圆O的直径,点C是半圆O上不同于 的一点,点D为弧 的中点,连结 ,设 ,则( ).
 A、 B、 C、 D、6. 如图,⊙O的直径长10,弦AB=8,M是弦AB上的动点,则OM的长的取值范围是( )
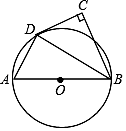
A、 B、 C、 D、6. 如图,⊙O的直径长10,弦AB=8,M是弦AB上的动点,则OM的长的取值范围是( ) A、3≤OM≤5 B、4≤OM≤5 C、3<OM<5 D、4<OM<57. 如图,已知C、D在以AB为直径的⊙O上,若∠CAB=30°,则∠D的度数是( )
A、3≤OM≤5 B、4≤OM≤5 C、3<OM<5 D、4<OM<57. 如图,已知C、D在以AB为直径的⊙O上,若∠CAB=30°,则∠D的度数是( )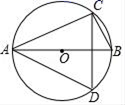 A、30° B、70° C、75° D、60°8. 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )米
A、30° B、70° C、75° D、60°8. 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )米 A、5 B、8 C、12 D、139. 如图, 是 的直径, 切 于点 , 交 于点 ;连接 ,若 ,则 等于( )
A、5 B、8 C、12 D、139. 如图, 是 的直径, 切 于点 , 交 于点 ;连接 ,若 ,则 等于( )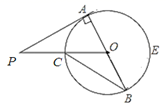 A、20° B、25° C、30° D、40°10. 如图,AB为⊙O的直径,点C在⊙O上,若 , ,则 的长为( )
A、20° B、25° C、30° D、40°10. 如图,AB为⊙O的直径,点C在⊙O上,若 , ,则 的长为( )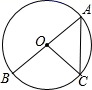 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,AB是半圆的直径,O是圆心, ,则∠ABC=°.
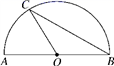 12. 扇形的半径为9,圆心角为120°,则它的弧长为.13. 如图,在⊙O中,∠ABC=50°,则∠AOC等于
12. 扇形的半径为9,圆心角为120°,则它的弧长为.13. 如图,在⊙O中,∠ABC=50°,则∠AOC等于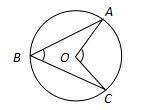 14. 如图, 、 、 是半径为3的 上的三点,已知 ,则劣弧 的长为.
14. 如图, 、 、 是半径为3的 上的三点,已知 ,则劣弧 的长为. 15. AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BOC=50°,则∠D的度数为.
15. AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BOC=50°,则∠D的度数为.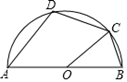 16. 如图,AB是⊙O的直径,点C、D在半圆AB上,且 ,连接AC、AD,则∠CAD的度数是°.
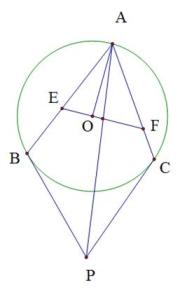
16. 如图,AB是⊙O的直径,点C、D在半圆AB上,且 ,连接AC、AD,则∠CAD的度数是°. 17. 如图, 、 、 分别切 于点 、 、 , 交 、 于点 、 ,已知 长 ,则 的周长为.
17. 如图, 、 、 分别切 于点 、 、 , 交 、 于点 、 ,已知 长 ,则 的周长为.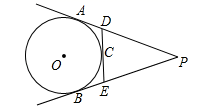 18. 如图,AB为⊙O的直径,C为⊙O上一点,其中AB=2,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为.
18. 如图,AB为⊙O的直径,C为⊙O上一点,其中AB=2,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为.
三、解答题
-
19. 已知:A、B、C、D是⊙O上的四个点,且 ,求证:AC=BD .
 20. 如图,AD,BC是⊙O的两条弦,且AD=BC,求证:AB=CD.
20. 如图,AD,BC是⊙O的两条弦,且AD=BC,求证:AB=CD. 21. 如图, 是 的弦,半径 ,点 在 上,且 .求 的度数.
21. 如图, 是 的弦,半径 ,点 在 上,且 .求 的度数. 22. 如图,AB是⊙O直径,弦CD与AB相交与点E , ∠ADC=26°,求∠CAB的度数.
22. 如图,AB是⊙O直径,弦CD与AB相交与点E , ∠ADC=26°,求∠CAB的度数.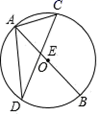 23. 如图, 内接于 , , ,则 的直径等于多少?
23. 如图, 内接于 , , ,则 的直径等于多少?