甘肃省兰州市教学管理第五片区2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2021-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数是无理数的是（）

A、﹣1 B、 $\sqrt{3}$ C、3.14 D、 $\frac{1}{3}$

查看试题解析
2. 在平面直角坐标系中，点M（﹣2，1）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知 ${\begin{array}{l} x = a \\ y = - 2 \end{array}$ 是关于x，y的方程3x﹣ay＝5的一个解，则a的值为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 已知|a﹣6|+|b﹣8|+（c﹣10）²＝0，则以a，b，c为三边长的三角形是（）

A、直角三角形 B、锐角三角形 C、等腰三角形 D、钝角三角形

查看试题解析
5. 平面直角坐标系中，点P（﹣2，3）关于x轴对称的点的坐标为（　　）

A、（﹣2，﹣3） B、（2，﹣3） C、（﹣3，﹣2） D、（3，﹣2）

查看试题解析
6. 如图， $l_{1} ∥ l_{2}$ ，∠1=54°，则∠2的度数为（）

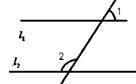A、36° B、54° C、126° D、144°

查看试题解析

7. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：

	甲	乙	丙	丁
平均数（cm）	185	180	185	180
方差	3.6	3.6	7.4	8.1

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

8. 某一次函数的图象经过点（1，2），且y随x的增大而减小，则这个函数的表达式可能是（）

A、 $y = 2 x + 4$ B、 $y = 3 x - 1$ C、 $y = - 3 x + 1$ D、 $y = - 2 x + 4$

查看试题解析
9. 下列计算正确的是（）

A、 $\sqrt{{(- 9)}^{2}}$ ＝－9 B、 $\sqrt{25}$ ＝±5 C、 $\sqrt[3]{{(- 1)}^{3}}$ ＝－1 D、(－ $\sqrt{2}$ )²＝4

查看试题解析
10. 下列命题中真命题是（）

A、若a²=b²,则a=b B、4的平方根是±2 C、两个锐角之和一定是钝角 D、相等的两个角是对顶角

查看试题解析
11. 我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空.”这首诗的意思是说：如果一间客房住 $7$ 个人，那么就剩下 $7$ 个人安排不下；如果一间客房住 $9$ 个人，那么就空出一间客房.问现有客房多少间？房客多少人？设现有客房间x，房客人y，则可列方程组（）

A、 ${\begin{array}{l} 7 x - 7 = y \\ 9 (x + 1) = y \end{array}$ B、 ${\begin{array}{l} 7 x + 7 = y \\ 9 (x - 1) = y \end{array}$ C、 ${\begin{array}{l} 7 x - 7 = y \\ 9 (x - 1) = y \end{array}$ D、 ${\begin{array}{l} 7 x + 7 = y \\ 9 (x + 1) = y \end{array}$

查看试题解析
12. 一次函数 $y_{1} = k x + b$ 与 $y_{2} = x + a$ 的图象如图所示，给出下列结论：① $k < 0$ ；② $a > 0$ ；③当 $x < 3$ 时， $y_{1} < y_{2}$ .其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

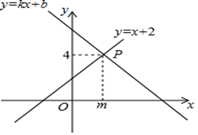
13. 最简二次根式 $\sqrt{2 b + 1}$ 与 $\sqrt{7 - b}$ 是同类二次根式，则b= ．

查看试题解析
14. 如图，一次函数y＝kx+b与y＝x+2的图象相交于点P（m，4），则关于x，y的二元一次方程组 ${\begin{array}{l} k x - y = - b \\ y - x = 2 \end{array}$ 的解是。

查看试题解析
15. 如图△ABC中，∠A=90°，点D在AC边上，DE∥BC，若∠1=155°，则∠B的度数为.

查看试题解析
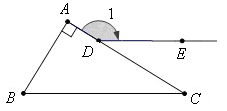16. 如图，有一矩形纸片OABC放在直角坐标系中，O为原点，C在x轴上，OA＝6，OC＝10，如图，在OA上取一点E，将△EOC沿EC折叠，使O点落在AB边上的D点处，则点E的坐标为。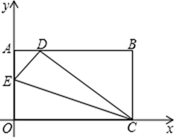

查看试题解析

三、解答题

17. 计算：

(1)、 $\frac{\sqrt{12} - \sqrt{24}}{\sqrt{6}} + (\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})$

(2)、 ${(- 1)}^{2017} + \sqrt{4} - | - \sqrt{3} | - {(2 - 2016)}^{0}$

查看试题解析
18. 解方程组

(1)、 ${\begin{array}{l} 6 x - 5 y = 3 \\ 6 x + y = - 15 \end{array}$

(2)、 ${\begin{array}{l} 3 (x - 1) = y + 5 \\ 5 (y - 1) = 3 (x + 5) \end{array}$

查看试题解析
19. 兰州市外国语学校开展“数学史”知识竞赛活动，八年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如图所示：

(1)、请计算八（1）班、八（2）班选出的5名选手复赛的平均成绩？众数和中位数？

(2)、请用方差判断哪个班选出的5名选手的复赛成绩比较稳定？

查看试题解析
20. 如图，在一次夏令营活动中，小明从营地A出发，沿北偏东60°方向走了 $50 \sqrt{3}$ m 到达点B，然后再沿北偏西30°方向走了50m到达目的地C.

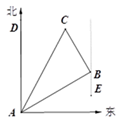(1)、求A、C两点之间的距离；

(2)、确定目的地C在营地A的北偏东多少度方向.

查看试题解析
21. 如图，已知∠1+∠2＝180°，∠3＝B，

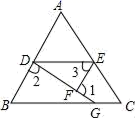(1)、证明：EF∥AB.

(2)、试判断∠AED与∠C的大小关系，并说明你的理由.

查看试题解析
22. 如图，是规格为8×8的正方形网格，请在所给网格中按下列要求操作：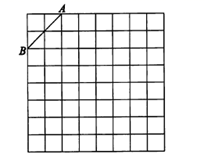

( 1 )在网格中建立平面直角坐标系，使A点坐标为(-2，4)，B点坐标为(-4，2)；

( 2 )在(1)的前提下，在第二象限内的格点上找一点C，使点C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点的坐标是；

( 3 )求((2)中△ABC的周长(结果保留根号)；

( 4 )画出((2)中△ABC关于y轴对称的△A'B'C'.

查看试题解析
23. 在元旦期间，某商场投入13800元资金购进甲、乙两种商品共500件，两种商品的成本价和销售价如下表所示：

商品

单价（元/件）

成本价

销售价

甲

24

36

乙

33

48

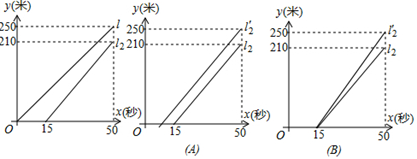
(1)、该商场购进两种商品各多少件？

(2)、这批商品全部销售完后，该商场共获利多少元？

查看试题解析
24. 如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点N沿路线O→A→C运动.

(1)、求直线AB的解析式.

(2)、求△OAC的面积.

(3)、当△ONC的面积是△OAC面积的 $\frac{1}{4}$ 时，求出这时点N的坐标.

查看试题解析
25. 小华和小峰是两名自行车爱好者，小华的骑行速度比小峰快 $.$ 两人准备在周长为250米的赛道上进行一场比赛 $.$ 若小华在小峰出发15秒之后再出发，图中 $l_{1}$ 、 $l_{2}$ 分别表示两人骑行路程与时间的关系．

(1)、小峰的速度为米 $/$ 秒，他出发米后，小华才出发；

(2)、小华为了能和小峰同时到达终点，设计了两个方案，方案一：加快骑行速度；方案二：比预定时间提前出发．
①图 $($ 填“A“”或“B“ $)$ 代表方案一；

②若采用方案二，小华必须在小峰出发多久后开始骑行？求出此时小华骑行的路程与时间的函数关系式．

查看试题解析
26. 如图，在平面直角坐标系中，直线l₁的解析式为y=x，直线l₂的解析式为 $y = - \frac{1}{2} x + 3$ ，与x轴、y轴分别交于点A、点B，直线l₁与l₂交于点C．

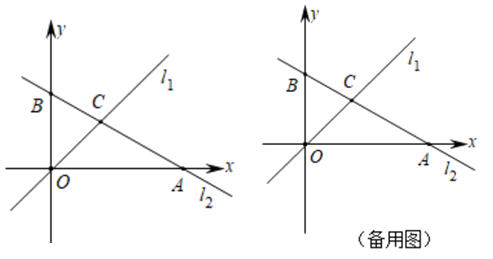(1)、求点A、点B、点C的坐标，并求出△COB的面积；

(2)、若直线l₂上存在点P(不与B重合)，满足S_△COP=S_△COB ，请求出点P的坐标；

(3)、在y轴右侧有一动直线平行于y轴，分别与l₁ ， l₂交于点M、N，且点M在点N的下方，y轴上是否存在点Q，使△MNQ为等腰直角三角形?若存在，请直接写出满足条件的点Q的坐标；若不存在，请说明理由．

查看试题解析