浙江省绍兴市柯桥区联盟校2021届九年级上学期数学1月月考试试卷

试卷更新日期：2021-02-23 类型：月考试卷

进入出卷网下载

一、选择题（每小题4分，共40分）

1. 若 $\frac{a}{b} = \frac{1}{2}$ ，则 $\frac{a}{a + b}$ 的值是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
2. 抛物线y＝（x+1）²+2的顶点是（）

A、（1，2） B、（﹣1，2） C、（﹣1，﹣2） D、（1，﹣2）

查看试题解析
3. 甲、乙两名同学在一次用频率去估计概率的实验中，统计了某一结果出现的频率绘出的统计图如图所示，则符合这一结果的实验可能是（　　）

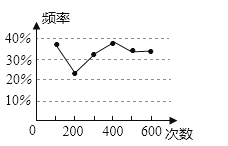A、掷一枚正六面体的骰子，出现1点的概率 B、从一个装有2个白球和1个红球的袋子中任取一球，取到红球的概率 C、抛一枚硬币，出现正面的概率 D、任意写一个整数，它能被2整除的概率

查看试题解析
4. 已知函数y＝x²+2x+4上的三点（﹣2015，y₁），（2014，y₂），（2015，y₃），则下列选项正确的是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₂＜y₃＜y₁ D、y₃＜y₁＜y₂

查看试题解析
5. 如图，在△ABC中，点D ， E分别在边AC ， BC上，则不一定能判断△ABC∽△EDC的是（）

A、∠CDE＝∠B B、∠DEC＝∠A C、 $\frac{C D}{E C} = \frac{C B}{A C}$ D、 $\frac{C D}{B C} = \frac{D E}{B A}$

查看试题解析
6. 请你运用学过的函数知识，判断下列哪一个图象可能是函数y＝x³的图象（）

A、 B、 C、 D、

查看试题解析
7. 如图，⊙O是△ABC的外接圆，若∠AOB＝110°，则∠ACB的度数是（）

A、55° B、70° C、125° D、110°

查看试题解析
8. 如图，在边长为6的菱形ABCD中，∠DAB＝60°，以点D为圆心，菱形的高DF为半径画弧，交AD于点E ，交CD于点G ，则图中阴影部分的面积是（）

A、18 $\sqrt{3}$ ﹣9π B、18﹣3π C、9 $\sqrt{3}$ ﹣ D、18 $\sqrt{3}$ ﹣3π

查看试题解析
9. 如图，在平面直角坐标系中，以原点O为圆心，3为半径的半圆，直线AB：y＝x+b与x轴交于点P（x ， 0），若直线AB与半圆弧有公共点，则x值的范围是（）

A、﹣3≤x≤3 $\sqrt{2}$ B、﹣3≤x≤3 C、﹣3 $\sqrt{2}$ ≤x≤3 D、0≤x≤3 $\sqrt{2}$

查看试题解析
10. 如图，已知点C在以AB为直径的⊙O上，点D在AB的延长线上，∠BCD＝∠A ，过点C作CE⊥AB于E ， CE＝8，cosD＝ $\frac{4}{5}$ ，则AC的长为（）

A、8 $\sqrt{5}$ B、8 $\sqrt{3}$ C、10 D、8 $\sqrt{2}$

查看试题解析

二、填空题（每小题5分，共30分）

11. 圆内接四边形ABCD中，∠A：∠B：∠C＝1：2：4，则∠D＝度．

查看试题解析
12. 若线段c是线段a和b的比例中项，且a＝2cm ， b＝8cm ，则线段c的长是cm ．

查看试题解析
13. 如图，△ABC的顶点是正方形网格的格点，则tanA的值为．

查看试题解析
14. 如图，△ABC内接于⊙O ， DA切⊙O于点A ，交BC的延长线于点D ．若∠B＝25°，∠ACB＝80°，则∠D的度数为度．

查看试题解析
15. 如图，直线l₁⊥l₂ ，垂足为O ，点A、B分别在直线l₁和l₂上，∠OAB＝30°，OB＝2，以A为圆心，1为半径画圆，点P在圆A的圆周上运动，连接AP ，过点P画PA的垂线与线段AB相交于点C ，与直线l₂相交于D ，当AC＝BC时，OD的长是．

查看试题解析
16. 如图，已知抛物线y＝ax²+bx（a≠0）经过A（3，0）、B（4，4）两点．

(1)、抛物线的解析式为；

(2)、若点D、N均在此抛物线上，其中点D坐标为（2，﹣2），点N满足∠NBO＝∠ABO ， P为平面上一点，则所有满足△POD∽△NOB的点P的坐标有（点P、O、D分别与点N、O、B对应）．

查看试题解析

三、解答题（本大题共8小题，共80分）

17. 如图，一个转盘被分成3等分，每一份上各写有一个数字，随机转动转盘2次，第一次转到的数字数字为十位数字，第二次转到的数字为个位数字，2次转动后组成一个两位数（若指针停在等分线上则重新转一次）

(1)、用画树状图的方法求出转动后所有可能出现的两位数的个数．

(2)、甲、乙两人做游戏，约定得到的两位数是偶数时甲胜，否则乙胜，这个游戏公平吗？请说明理由．

查看试题解析
18. 如图，从点A看一山坡上的电线杆PQ，观测点P的仰角是45°，向前走6m到达B点，测得顶端点P和杆底端点Q的仰角分别是60°和30°，求该电线杆PQ的高度．

查看试题解析
19. 如图，点D是半径为R的⊙O上一点．

(1)、若∠A＝∠C＝30°，求证：直线CD与⊙O相切；

(2)、已知直线CD与⊙O相切，下列条件：①AD＝CD；②∠A＝30°；③∠ADC＝120°；④DC＝ $\sqrt{3}$ R ．其中能得出BC＝R的是哪几个？并给出你认为能得出的第一个（按编号顺序）的说理过程．

查看试题解析
20. 如图，已知点A（0，4）和点B（3，0）都在抛物线y＝mx²+2mx+n上．

(1)、求m、n；

(2)、向右平移上述抛物线，记平移后点A的对应点为D ，点B的对应点为C ，若四边形ABCD为菱形，求平移后抛物线的表达式；

查看试题解析
21. 宁波地区最近雾霾天气频繁，使得空气净化器得以畅销，某商场代理销售某种空气净化器，其进价是500元/台，经过市场销售后发现，在一个月内，当售价是1000元/台时，可售出50台，且售价每降低20元，就可多售出5台．若供货商规定这种空气净化器售价不能低于600元/台，代理销售商每月要完成不低于60台的销售任务．

(1)、试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围；

(2)、当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？

查看试题解析
22. 在平面直角坐标系中，对于任意一点P（x ， y），我们做以下规定：d（P）＝|x|+|y|，称d（P）为点P的坐标距离．

(1)、已知：点A（3，﹣4），求点A的坐标距离d（A）的值．

(2)、如图，四边形OABC为矩形，点A ， B在第一象限，且OC：OA＝1：2．
①求证：d（A）＝d（C）×2

②若OC＝2，且满足d（A）+d（C）＝d（B）+2，求点B坐标．

查看试题解析
23. 如图1，在△APE中，∠PAE＝90°，PO是△APE的角平分线，以O为圆心，OA为半径作圆交AE于点G ．

(1)、求证：直线PE是⊙O的切线；

(2)、在图2中，设PE与⊙O相切于点H ，连结AH交PO于点D ，已知PA＝6，tan∠EAH＝ $\frac{2}{3}$ ．
①求⊙O的半径；

②求EH的长．

查看试题解析
24. 在平面直角坐标系中，已知抛物线y＝﹣x²+bx+c与x轴交于A、B两点（点A在点B左边），与y轴交于点C ， ⊙M是△ABC的外接圆．
如图1，若抛物线的顶点D的坐标为（1，4）

(1)、求抛物线的解析式，及A、B、C三点的坐标；

(2)、求⊙M的半径和圆心M的坐标．

(3)、如图2，在x轴上有点P（7，0），试在直线BC上找点Q ，使B、Q、P三点构成的三角形与△ABC相似．若存在，请求出Q点坐标；若不存在，请说明理由．

(4)、向上平移抛物线y＝﹣x²+bx+c ，在平移过程中，抛物线与x轴交于A′、B′两点，与y轴交于点C′，则△A′B′C′的外接圆⊙M′是否经过一个定点？若是，请求出这个点的坐标；若不是，请说明理由．

查看试题解析