浙江省余姚市2021届九年级上学期数学第三次月考试卷
试卷更新日期:2021-02-23 类型:月考试卷
一、选择题(每小题4分,共48分)
-
1. 下列事件中,属于不可能事件的是( )A、明天会下雨 B、从只装有8个白球的袋子中摸出红球 C、抛一枚硬币正面朝上 D、在一个标准大气压下,加热到100℃水会沸腾2. 若 ,则 ( )A、 B、 C、 D、3. 将二次函数y=(x﹣1)2+2的图象向下平移3个单位,得到的图象对应的表达式是( )A、y=(x+2)2+2 B、y=(x﹣4)2+2 C、y=(x﹣1)2﹣1 D、y=(x﹣1)2+54. 在正面完全相同、反面印有下列四个图形的纸片中,任抽一张,则抽到的图形中,既是轴对称图形,又是中心对称图形的概率是( )
 A、 B、 C、 D、15. 如图,圆 半径为 ,弓形高为 ,则弓形的弦 的长为( )
A、 B、 C、 D、15. 如图,圆 半径为 ,弓形高为 ,则弓形的弦 的长为( ) A、 B、 C、 D、6. 如图,在△ABC中,DE∥BC分别交AB,AC于点D,E,若 = ,则下列说法不正确的是( )
A、 B、 C、 D、6. 如图,在△ABC中,DE∥BC分别交AB,AC于点D,E,若 = ,则下列说法不正确的是( ) A、 = B、 = C、 = D、 =7. 已知点A(3,y1)、B(﹣2,y2)、C(2,y3)在二次函数y=x2﹣2x+b的图象上,则y1 , y2 , y3的大小关系为( )A、y1<y3<y2 B、y2<y1<y3 C、y3<y2<y1 D、y3<y1<y28. 二次函数y=﹣x2+2x+4,当﹣1≤x≤2时,则( )A、1≤y≤4 B、y≤5 C、4≤y≤5 D、1≤y≤59. 如图,用若n个全等的正五边形按如下方式拼接可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为24°,图中所示的是前3个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形,则n的值为( )
A、 = B、 = C、 = D、 =7. 已知点A(3,y1)、B(﹣2,y2)、C(2,y3)在二次函数y=x2﹣2x+b的图象上,则y1 , y2 , y3的大小关系为( )A、y1<y3<y2 B、y2<y1<y3 C、y3<y2<y1 D、y3<y1<y28. 二次函数y=﹣x2+2x+4,当﹣1≤x≤2时,则( )A、1≤y≤4 B、y≤5 C、4≤y≤5 D、1≤y≤59. 如图,用若n个全等的正五边形按如下方式拼接可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为24°,图中所示的是前3个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形,则n的值为( )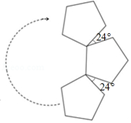 A、5 B、6 C、8 D、1010. 如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( )
A、5 B、6 C、8 D、1010. 如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC为半径画弧,交数轴于点P,则OP的中点D对应的实数是( ) A、 B、 C、 D、11. 如图,△OAC按顺时针方向旋转,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把△OAC绕点A按顺时针方向转到△O′AC′,使得点O′的坐标是(4, )则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为( )
A、 B、 C、 D、11. 如图,△OAC按顺时针方向旋转,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把△OAC绕点A按顺时针方向转到△O′AC′,使得点O′的坐标是(4, )则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为( )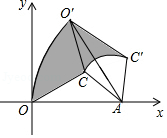 A、 B、 C、 D、12. 如图, 为⊙O直径 上一动点,过点 的直线交⊙O于 , 两点,且 , 于点 , 于点 ,当点 在 上运动时.设 , ,下列中图象中,能表示 与的函数关系式的图象大致是
A、 B、 C、 D、12. 如图, 为⊙O直径 上一动点,过点 的直线交⊙O于 , 两点,且 , 于点 , 于点 ,当点 在 上运动时.设 , ,下列中图象中,能表示 与的函数关系式的图象大致是 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(每小题4分,共24分)
-
13. 盒子里有4支红色笔芯,3支黑色笔芯,每支笔芯除颜色外均相同.从中任意摸出一支笔芯,则摸出黑色笔芯的概率是.14. 点C是线段AB的黄金分割点(AC>BC),AB=2,则AC=.(用根号表示)15. 已知扇形的弧长为 ,半径为 ,则此扇形的圆心角为度.16. 若二次函数:y=ax2+bx+c的x与y的部分对应值如表,则当x=1时,y的值为.
x
﹣7
﹣6
﹣5
﹣4
﹣3
﹣2
y
﹣27
﹣13
﹣3
3
5
3
17. 如图,抛物线y=ax2+c与直线y=3相交于点A、B,与y轴交于点C(0,﹣1),若∠ACB为直角,则当ax2+c<0时自变量x的取值范围是.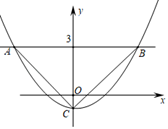 18. 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最大值为
18. 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最大值为
三、解答题(第19题6分,第20、21题8分,第22、23、24题10分,第25题12分,第26题14分,共78分)
-
19. 已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.(1)、求a、b、c的值;(2)、若线段x是线段a、b的比例中项,求x的值.20. 已知二次函数y=ax2+bx+3的图象经过点(﹣3,0),(2,﹣5).(1)、试确定此二次函数的解析式;(2)、请你判断点P(﹣2,3)是否在这个二次函数的图象上?21. 2018年6月,宁波全面推进生活垃圾分类工作,如图是某小区放置的垃圾桶,从左到右依次是绿色:厨余垃圾;蓝色:可回收垃圾;黑色:其他垃圾.红色:有害垃圾;
 (1)、居民A将一袋厨余垃圾随手放入一个垃圾桶,问他能正确投放垃圾的概率是.(2)、居民B手拎两袋垃圾,一袋是可回收垃圾,另一袋是有害垃圾,她先将可回收垃圾随手放入一个垃圾桶,然后把另一袋垃圾又随手放入其他垃圾桶.问:两袋垃圾都投放错误的概率?请画出树状图或列表说明理由.
(1)、居民A将一袋厨余垃圾随手放入一个垃圾桶,问他能正确投放垃圾的概率是.(2)、居民B手拎两袋垃圾,一袋是可回收垃圾,另一袋是有害垃圾,她先将可回收垃圾随手放入一个垃圾桶,然后把另一袋垃圾又随手放入其他垃圾桶.问:两袋垃圾都投放错误的概率?请画出树状图或列表说明理由.
22. 如图,已知AD=3cm,AC=6cm,BC=9cm,∠B=36°,∠D=117°,△ABC∽△DAC. (1)、求AB的长;(2)、求∠BAD的大小.23. 如图,AB是⊙O的直径,C是 的中点,CE⊥AB于点E,BD交CE于点F.
(1)、求AB的长;(2)、求∠BAD的大小.23. 如图,AB是⊙O的直径,C是 的中点,CE⊥AB于点E,BD交CE于点F. (1)、求证:CF=BF;(2)、若CD=6,AC=8,求⊙O的半径和线段CE,及EF的长.24. 某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间.经市场调查表明,该馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数y(间)与每间标准房的价格x(元)的数据如下表:
(1)、求证:CF=BF;(2)、若CD=6,AC=8,求⊙O的半径和线段CE,及EF的长.24. 某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间.经市场调查表明,该馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数y(间)与每间标准房的价格x(元)的数据如下表:x(元)
…
190
200
210
220
…
y(间)
…
65
60
55
50
…
 (1)、根据所给数据在坐标系中描出相应的点,并画出图形(2)、求y关于x的函数表达式,并写出自变量x的取值范围.(3)、设客房的日营业额为w(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?25. 定义:对角线互相垂直的圆内接四边形叫做圆的奇妙四边形.
(1)、根据所给数据在坐标系中描出相应的点,并画出图形(2)、求y关于x的函数表达式,并写出自变量x的取值范围.(3)、设客房的日营业额为w(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?25. 定义:对角线互相垂直的圆内接四边形叫做圆的奇妙四边形. (1)、如图①,已知四边形ABCD是⊙O的奇妙四边形,若AC=6,BD=8,则S四边形ABCD=;(2)、如图②,已知四边形ABCD内接于⊙O,对角线交于点E,若 + =180°,
(1)、如图①,已知四边形ABCD是⊙O的奇妙四边形,若AC=6,BD=8,则S四边形ABCD=;(2)、如图②,已知四边形ABCD内接于⊙O,对角线交于点E,若 + =180°,①求证:四边形ABCD是⊙O的奇妙四边形;
②作OM⊥BC于M,请猜想AD与OM之间的数量关系,并推理说明.
26. 已知抛物线与x轴交于点A(﹣2,0)、B(3,0),与y轴交于点C(0,4). (1)、求抛物线的解析式;(2)、如图1,点P是抛物线上位于第一象限内的一点,当四边形ABPC的面积最大时,求出四边形ABPC的面积最大值及此时点P的坐标.(3)、如图2,将抛物线向右平移 个单位,再向下平移2个单位.记平移后的抛物线为y',若抛物线y'与原抛物线对称轴交于点Q.点E是新抛物线y'对称轴上一动点,在(2)的条件下,当△PQE是等腰三角形时,求点E的坐标.
(1)、求抛物线的解析式;(2)、如图1,点P是抛物线上位于第一象限内的一点,当四边形ABPC的面积最大时,求出四边形ABPC的面积最大值及此时点P的坐标.(3)、如图2,将抛物线向右平移 个单位,再向下平移2个单位.记平移后的抛物线为y',若抛物线y'与原抛物线对称轴交于点Q.点E是新抛物线y'对称轴上一动点,在(2)的条件下,当△PQE是等腰三角形时,求点E的坐标.