浙江省绍兴市柯桥区联盟校2020-2021学年七年级上学期数学1月月考试卷

试卷更新日期：2021-02-23 类型：月考试卷

进入出卷网下载

一、选择题（共10题；共20分）

1. 2019的倒数是（）

A、 2019 B、﹣2019 C、 $\frac{1}{2019}$ D、 $- \frac{1}{2019}$

查看试题解析
2. 火星和地球的距离约为34 000 000千米，用科学记数法表示34 000 000的结果是（）千米．

A、0.34×10⁸ B、3.4×10⁶ C、34×10⁶ D、3.4×10⁷

查看试题解析
3. 如图，张亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是（）

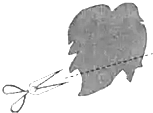A、经过一点有无数条直线 B、经过两点，有且仅有一条直线 C、两点间距离的定义 D、两点之间，线段最短

查看试题解析
4. 下列说法错误的是（）

A、3²x²y²的次数是6 B、x的系数、次数都是1 C、﹣的系数是﹣ D、0是单项式

查看试题解析
5. 下列各组单项式中，不是同类项的是（）

A、4a²y与 $\frac{2 y a^{2}}{3}$ B、xy³与﹣xy³ C、2abx²与x²ba D、7a²n与﹣9an²

查看试题解析
6. 下列化简正确的是（）

A、2a+3b＝5ab B、7ab﹣3ab＝4 C、2ab+3ab＝5ab D、a²+a²＝a⁴

查看试题解析
7. 估计 $\sqrt{11} + 2$ 的值在（）

A、3到4之间 B、4到5之间 C、5到6之间 D、6到7之间

查看试题解析
8. 代数式2ax+5b的值会随x的取值不同而不同，如表是当x取不同值时对应的代数式的值，则关于x的方程2ax+5b＝﹣4的解是（）

x

﹣4

﹣3

﹣2

﹣1

0

2ax+5b

12

8

4

0

﹣4

A、12 B、4 C、﹣2 D、0

查看试题解析
9. 一套仪器由一个A部件和三个B部件构成，用1m³钢材可做40个A部件或240个B部件，现要用6m³钢材制作这种仪器，设应用xm³钢材做B部件，其他钢材做A部件，恰好配套，则可列方程为（）

A、3×40x＝240（6﹣x） B、240x＝3×40（6﹣x） C、40x＝3×240（6﹣x） D、3×240x＝40（6﹣x）

查看试题解析
10. 如图，圆上有五个点，这五个点将圆分成五等份（每一份称为一段弧长），把这五个点按顺时针方向依次编号为1，2，3，4，5，若从某一点开始，沿圆周顺时针方向行走，点的编号是数字几，就走几段弧长，我们把这种走法称为一次“移位”.如：小明在编号为3的点，那么他应走3段弧长，即从3→4→5→1为第1次“移位”，这时他到达编号为1的点，那么他应走1段弧长，即从1→2为第2次“移位”.若小明从编号为4的点开始，经过2020次“移位”后，他到达编号为（）

A、1 B、2 C、4 D、5

查看试题解析

二、填空题（共10题；共30分）

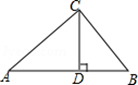
11. 9的算术平方根是．

查看试题解析
12. 近似数8.28万的精确到位.

查看试题解析
13. 单项式﹣ $\frac{2 π x^{2} y}{5}$ 的系数是.

查看试题解析
14. 若∠α＝60°42'，则它的余角的度数是.

查看试题解析
15. 如图，AC⊥BC，垂足为点C，CD⊥AB，垂足为点D，则点B到AC的距离是线段的长度.

查看试题解析
16. 若x＝﹣1是关于x的方程2x﹣a+2b＝0的解，则代数式2a﹣4b+1的值是.

查看试题解析
17. 已知a，b，c在数轴上的位置如图所示，化简：|a﹣b|+|b+c| - |c﹣a|＝.

查看试题解析
18. 如图，将一张长方形纸片分别沿着EP，FP对折，使点B落在点B，点C落在点C′.若点P，B′，C′不在一条直线上，且两条折痕的夹角∠EPF＝85°，则∠B′PC′＝.

查看试题解析
19. 如图，一个盛有水的圆柱形玻璃容器的内底面半径为10cm，容器内水的高度为12cm.把一根半径为2cm的玻璃棒垂直插入水中，则容器内的水将升高cm（假设水不会溢出）.

查看试题解析
20. 如图，点A、O、B都在直线MN上，射线OA绕点O按顺时针方向以每秒4°的速度旋转，同时射线OB绕点O按逆时针方向以每秒6°的速度旋转（当其中一条射线与直线MN叠合时，两条射线停止旋转）.经过秒，∠AOB的大小恰好是60°.

查看试题解析

三、解答题（共8小题）

21. 计算：

(1)、 $（ \frac{1}{3} - \frac{1}{4} ） \times 12 + （ - 3 ）^{2}$

(2)、 $- 2^{3} + \sqrt[3]{8} \div （ - 8 ） \times \sqrt{64}$

查看试题解析
22. 解方程（组）：

(1)、 ${\begin{cases} 4x-y = 8 \\ 3x + y = 13 \end{cases}$

(2)、 $\frac{3 y - 1}{2} - 1 = \frac{5 y - 7}{3}$

查看试题解析
23. 化简并求值：2（a²﹣ab）﹣3（b²﹣ab），其中a＝﹣3，b＝3.

查看试题解析
24. 光明中学组织学生到距离学校9千米的博物馆参观，学生小华因有事未能上包车，于是准备在学校门口直接乘出租车去博物馆，出租车的收费标准如下：

里程

收费（元）

3千米以内（含3千米）

10.00

3千米以外，每增加1千米

2.40

(1)、写出小华乘出租车的里程数为x千米（x≥3）时，所付车费为多少元？（用含x的代数式表示）；

(2)、如果小华同学身上仅有25元钱，由学校乘出租车到博物馆钱够不够？请说明理由.

查看试题解析
25. 我们称使方程 $\frac{x}{2} + \frac{y}{3} = \frac{x + y}{2 + 3} + 1$ 成立的一对数x，y为“相伴数对”，记为（x.y）.

(1)、若（4，y）是“相伴数对”，求y的值；

(2)、若（a，b）是“相伴数对”，请用含b的代数式表示a；

查看试题解析
26. 已知点O是直线AB上一点，∠COD是直角，OE平分∠BOC.

(1)、如图，若∠AOC＝40°，求∠DOE的度数；

(2)、如图，若∠AOC＝a，求∠DOE的度数。（用含a的代数式表示）

查看试题解析
27. 如图，用正方形硬纸板做三棱柱盒子，每个盒子由3个长方形侧面和2个正三角形底面组成.硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）.

A方法：剪6个侧面；

B方法：剪4个侧面和5个底面.

现有38张硬纸板，裁剪时x张用A方法，其余用B方法.

(1)、分别求裁剪出的侧面和底面的个数（用x的代数式表示）

(2)、若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？

查看试题解析
28. 如图，点A、B和线段CD都在数轴上，点A、C、D、B起始位置所表示的数分别为﹣2、0、3、12；线段CD沿数轴的正方向以每秒1个单位的速度移动，移动时间为t秒.

(1)、当t＝0秒时，AC的长为，当t＝2秒时，AC的长为.

(2)、用含有t的代数式表示AC的长为.

(3)、当t＝秒时AC﹣BD＝5，当t＝秒时AC+BD＝15.

(4)、若点A与线段CD同时出发沿数轴的正方向移动，点A的速度为每秒2个单位，在移动过程中，是否存在某一时刻使得AC＝2BD，若存在，请求出t的值；若不存在，请说明理由.

查看试题解析

里程	收费（元）
3千米以内（含3千米）	10.00
3千米以外，每增加1千米	2.40

x	﹣4	﹣3	﹣2	﹣1	0
2ax+5b	12	8	4	0	﹣4