浙江省温州市2020-2021学年八年级上学期数学期末考试试卷(A)
试卷更新日期:2021-02-23 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 满足-1<x≤2的数在数轴上表示为( ).A、
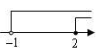 B、
B、 C、
C、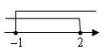 D、
D、 2. 下面四幅图是我国一些博物馆的标志,其中属于轴对称图形的是 ( )A、
2. 下面四幅图是我国一些博物馆的标志,其中属于轴对称图形的是 ( )A、 B、
B、 C、
C、 D、
D、 3. 如图所示,在△ABC中,AB = AC,D是BC中点,下列结论中,不正确的是( )
3. 如图所示,在△ABC中,AB = AC,D是BC中点,下列结论中,不正确的是( ) A、∠B = ∠C B、AD⊥BC C、AD平分∠BAC D、AB = 2BD4. 如图所示,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A、∠B = ∠C B、AD⊥BC C、AD平分∠BAC D、AB = 2BD4. 如图所示,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )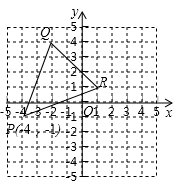 A、( - 2, - 4) B、( - 2,4) C、(2, - 3) D、( - 1, - 3)5. 小莹和小博下棋,小莹执白,小博执黑.如图所示,棋盘中心黑子的位置用( - 1,0)表示,右下角黑子的位置用(0, - 1)表示.小莹将第4枚白子放人棋盘后,所有棋子构成一个轴对称图形,她放的位置是( )
A、( - 2, - 4) B、( - 2,4) C、(2, - 3) D、( - 1, - 3)5. 小莹和小博下棋,小莹执白,小博执黑.如图所示,棋盘中心黑子的位置用( - 1,0)表示,右下角黑子的位置用(0, - 1)表示.小莹将第4枚白子放人棋盘后,所有棋子构成一个轴对称图形,她放的位置是( ) A、( - 2,1) B、( - 1,1) C、(1, - 2) D、( - 1, - 2)6. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图所示,一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的平分线.”他这样作的依据是( )
A、( - 2,1) B、( - 1,1) C、(1, - 2) D、( - 1, - 2)6. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图所示,一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的平分线.”他这样作的依据是( )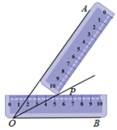 A、角平分线上的点到这个角两边的距离相等 B、角的内部到角的两边的距离相等的点在这个角的平分线上 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确7. 已知a、b、c为△ 的三边,且满足 ,则△ 是A、直角三角形 B、等边三角形 C、等腰三角形 D、不能确定8. 如图所示,在△ABC中,D为AB上一点,E为BC上一点,且AC = CD = BD = BE,∠A = 50°,则∠CDE的度数为( )
A、角平分线上的点到这个角两边的距离相等 B、角的内部到角的两边的距离相等的点在这个角的平分线上 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确7. 已知a、b、c为△ 的三边,且满足 ,则△ 是A、直角三角形 B、等边三角形 C、等腰三角形 D、不能确定8. 如图所示,在△ABC中,D为AB上一点,E为BC上一点,且AC = CD = BD = BE,∠A = 50°,则∠CDE的度数为( ) A、50° B、51° C、51.5° D、52.5°9. 如图所示,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y + 1),则y关于x的函数表达式为( )
A、50° B、51° C、51.5° D、52.5°9. 如图所示,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y + 1),则y关于x的函数表达式为( ) A、y = x B、y = - 2x - 1 C、y = 2x - 1 D、y = 1 - 2x10. 如图所示,在△ABC中,∠C = 90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,则下列结论:①AD平分∠CDE;②∠BAC = ∠BDE;③DE平分∠ADB;④若AC = 4BE,则S△ABC = 8S△BDE.其中正确的有( )
A、y = x B、y = - 2x - 1 C、y = 2x - 1 D、y = 1 - 2x10. 如图所示,在△ABC中,∠C = 90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,则下列结论:①AD平分∠CDE;②∠BAC = ∠BDE;③DE平分∠ADB;④若AC = 4BE,则S△ABC = 8S△BDE.其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题4分,共24分)
-
11. 如图所示为象棋盘的一部分,若“帅”位于点(2, - 1)上,“相”位于点(4, - 1)上,则“炮”所在的点的坐标是 .
 12. 若等腰三角形中有两边长分别为2和5,则这个三角形的周长为 .13. 若关于x的不等式(3a - 2)x < 2的解为x > ,则a的取值范围是 .14. 如图所示,在平面直角坐标系中,点P(x,y)是直线y = - x + 6上第一象限的点,点A的坐标是(4,0),O是坐标原点,△PAO的面积为S,则S关于x的函数表达式为 .
12. 若等腰三角形中有两边长分别为2和5,则这个三角形的周长为 .13. 若关于x的不等式(3a - 2)x < 2的解为x > ,则a的取值范围是 .14. 如图所示,在平面直角坐标系中,点P(x,y)是直线y = - x + 6上第一象限的点,点A的坐标是(4,0),O是坐标原点,△PAO的面积为S,则S关于x的函数表达式为 .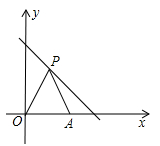 15. 如图所示,在Rt△ABC中,∠C = 90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD = 6,AB = 20,则△ABD的面积是 .
15. 如图所示,在Rt△ABC中,∠C = 90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD = 6,AB = 20,则△ABD的面积是 . 16. 当三角形中一个内角β是另一个内角a的 时,我们称此三角形为“希望三角形”,其中内角a称为“希望角”.如果一个“希望三角形”中有一个内角为54°,那么这个“希望三角形”的“希望角”度数为 .
16. 当三角形中一个内角β是另一个内角a的 时,我们称此三角形为“希望三角形”,其中内角a称为“希望角”.如果一个“希望三角形”中有一个内角为54°,那么这个“希望三角形”的“希望角”度数为 .三、解答题(共66分)
-
17. 解不等式 ,把它的解在数轴上表示出来,并写出该不等式的自然数解.18. 如图所示,已知点A( - 2,3),B(4,3),C( - 1, - 3).
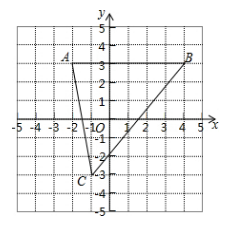 (1)、求点C到x轴的距离.(2)、求△ABC的面积.(3)、点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.19. 如图所示,已知一次函数y = 2x + a与y = - x + b的图象都经过点A( - 2,0),且与y轴分别交于B,C两点.
(1)、求点C到x轴的距离.(2)、求△ABC的面积.(3)、点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.19. 如图所示,已知一次函数y = 2x + a与y = - x + b的图象都经过点A( - 2,0),且与y轴分别交于B,C两点.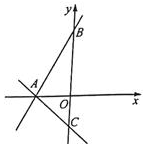 (1)、分别求出这两个一次函数的表达式.(2)、求△ABC的面积.20. 如图所示,在△ABC中,∠C = 2∠B,D为BC上一点且AD⊥AB,E是BD的中点,连结AE.
(1)、分别求出这两个一次函数的表达式.(2)、求△ABC的面积.20. 如图所示,在△ABC中,∠C = 2∠B,D为BC上一点且AD⊥AB,E是BD的中点,连结AE. (1)、求证:∠AEC = ∠C.(2)、求证:BD = 2AC.(3)、若AE = 8.5,AD = 8,求△ABE的周长.21. 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程y(km)与行驶的时间x(h)之间的函数关系如图1中线段AB所示,慢车离乙地的路程y(km)与行驶的时间x(h)之间的函数关系如图1中线段OC所示.根据图象进行以下研究.
(1)、求证:∠AEC = ∠C.(2)、求证:BD = 2AC.(3)、若AE = 8.5,AD = 8,求△ABE的周长.21. 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程y(km)与行驶的时间x(h)之间的函数关系如图1中线段AB所示,慢车离乙地的路程y(km)与行驶的时间x(h)之间的函数关系如图1中线段OC所示.根据图象进行以下研究.解读信息:
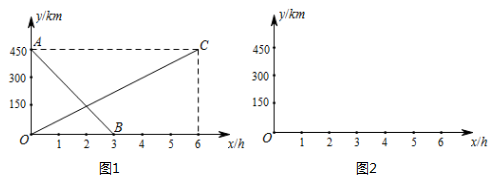 (1)、甲、乙两地之间的距离为 km.(2)、线段AB的函数表达式为 ;线段OC的函数表达式为 .(3)、问题解决:设快、慢车之间的距离为y(km),在图2中画出该函数的大致图象.22. 在直线上顺次取A,B,C三点,分别以AB,BC为边在直线的同侧作等边三角形,作得的两个等边三角形的另一顶点分别为D,E两点.连结DE.
(1)、甲、乙两地之间的距离为 km.(2)、线段AB的函数表达式为 ;线段OC的函数表达式为 .(3)、问题解决:设快、慢车之间的距离为y(km),在图2中画出该函数的大致图象.22. 在直线上顺次取A,B,C三点,分别以AB,BC为边在直线的同侧作等边三角形,作得的两个等边三角形的另一顶点分别为D,E两点.连结DE.

 (1)、如图1所示,连结CD,AE,求证:CD = AE.(2)、如图2所示,若AB = 1,BC = 2,求证:∠BDE = 90°.(3)、如图3所示,将图2中的等边三角形BEC绕点B作适当的旋转,连结AE,若有DE 2 + BE 2 = AE 2 , 试求∠DEB的度数.23. 如图所示,直线l1 , l2交于点C,直线l1与x轴交于点A;直线l2与x轴交于点B(3,0),与y轴交于点D(0,3),已知直线l1的函数表达式为y = 2x + 2.
(1)、如图1所示,连结CD,AE,求证:CD = AE.(2)、如图2所示,若AB = 1,BC = 2,求证:∠BDE = 90°.(3)、如图3所示,将图2中的等边三角形BEC绕点B作适当的旋转,连结AE,若有DE 2 + BE 2 = AE 2 , 试求∠DEB的度数.23. 如图所示,直线l1 , l2交于点C,直线l1与x轴交于点A;直线l2与x轴交于点B(3,0),与y轴交于点D(0,3),已知直线l1的函数表达式为y = 2x + 2. (1)、求直线l2的函数表达式和交点C的坐标.(2)、将直线l1向下平移a个单位使之经过点B,与y轴交于点E.
(1)、求直线l2的函数表达式和交点C的坐标.(2)、将直线l1向下平移a个单位使之经过点B,与y轴交于点E.①求△CBE的面积.
②若Q为y轴上一动点,当△EBQ为等腰三角形时,求出点Q的坐标.