浙江省杭州市2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-02-23 类型:期末考试
一、单选题(共30分)
-
1. 的相反数是( )A、2019 B、-2019 C、 D、2. 2019年国庆假期,全国民航运行总体安全平稳.据初步统计,7天共运送旅客1280万人次,同比增长约5.1%;平均客座率约84.9%.将1280万用科学记数法表示应为( )A、 B、 C、 D、3. 在下列各数0, , , , , 0.1010010001...(两个1之间,依次增加1个0),其中无理数有( )A、2个 B、3个 C、4个 D、5个4. 的算术平方根为( )A、13 B、±13 C、 D、5. 单项式 的次数是( )A、3 B、1 C、-3 D、46. 下列等式变形正确的是( )A、若 ,则 B、若 ,则 C、 ,则 D、若 ,则7. 已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )A、45° B、15° C、30°或60° D、45°或15°8. 若 ,则 的值为( )A、-6 B、-4 C、-3 D、49. 对于任意非零实数a, b,定义运算“※"如下: "a※b" = ,则1※2+ 2※3+ 3※4+…+ 2019※2020的值为( )A、 B、 C、 D、10. 如果,长方形 中有 个形状、大小相同的小长方形,且 , ,则图中阴影部分的面积为( ).
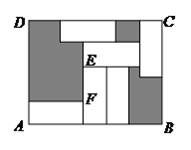 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共24分)
-
11. 比较大小: .12. 数轴上点P表示的数是﹣2,那么到P点的距离是3个单位长度的点表示的数是 .13. 一家三口准备参加一个旅游团外出旅游,甲旅行社告知:“父母买全票,女儿半价优惠.”乙旅行社告知:“家庭旅游按团体计价,即每人均按全价的80%收费.”假定两个旅行社每人的原票价相同,均为300元,小敏一家人从中选择了较便宜的一个旅游团参加了这次旅游,他们这次旅游付出了元的旅游团费.14. 的倒数为; 的算术平方根是.15. 如果 与 的和仍是单项式,则 .16. 方程 的解与关于x的方程 的解相同,则 .17. 如图,线段 表示一条已对折的绳子,现从 点处将绳子剪断,剪断后的各段绳子中最长的一段为 ,若 ,则原来绳长 .
 18. 归纳是数学思维中一种重要的推理方法.有一列数,按一定规律排成:0,-3,2,-6,4,-9,6,-12,8,…,观察此列数,若计a1=0,a2=-3,a3=2,….(1)、分析此规律,则a2018=;(2)、若有两个相邻数的和是-17,则这两个数分别是.
18. 归纳是数学思维中一种重要的推理方法.有一列数,按一定规律排成:0,-3,2,-6,4,-9,6,-12,8,…,观察此列数,若计a1=0,a2=-3,a3=2,….(1)、分析此规律,则a2018=;(2)、若有两个相邻数的和是-17,则这两个数分别是.三、解答题(共46分)
-
19. 在数轴上把数4,-2.5,0, 表示出来,并用“<”号把它们连结起来.20. 计算(1)、(2)、21.(1)、先化简,再求值: ,其中 , ;(2)、说明代数式 的值与 的取值无关.22. 数轴上A点对应的数是 ,B点在A点右边,电子蚂蚁甲,乙在B点分别以2个单位长度/秒,1个单位长度/秒的速度向左运动,电子蚂蚁丙在A点以3个单位长度/秒的速度向右运动.(1)、若电子蚂蚁丙经过5秒运动到C点,求C点表示的数;(2)、若B点表示的数为15,它们同时出发,请问丙遇到甲后多长时间丙遇到乙;(3)、在(2)的条件下,设它们同时出发的时间为t秒,是否存在t的值,使丙到乙的距离是丙到甲距离的2倍?若存在,求t的值;若不存在,说明理由.23. 已知数轴上三点M,O,N对应的数分别为 ,0,2,点P为数轴上任意一点,其对应的数为x.(1)、如果点P到点M,点N的距离相等,那么x的值是;(2)、数轴上是否存在点P,使点P到点M,点N的距离之和是7?若存在,请直接写出x的值,若不存在,请说明理由;
(3)、如果点P以每分钟3各单位长度的速度从点O向左运动时,点M和点N分别以每分钟1个单位长度和每分钟4个单位长度的速度也向左运动,且三点同时出发,那么几分钟时点P到点M,点N的距离相等.