河南省漯河市临颍县2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-02-23 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分）

1. 与算式 $3^{2} + 3^{2} + 3^{2}$ 的运算结果相等的是（）

A、 $3^{3}$ B、 $2^{3}$ C、 $3^{5}$ D、 $3^{6}$

查看试题解析
2. 如果 $x = 3$ 是方程 $\frac{1}{2} a + x = 2 x - a$ 的解，那么a的值为（）

A、2 B、6 C、-1 D、12

查看试题解析
3. 下列计算正确的是（）

A、 $3 a^{2} - a^{2} = 2$ B、 $2 m^{2} + m^{2} = 3 m^{4}$ C、 $3 m^{2} - 4 m^{2} = m^{2}$ D、 $- a b^{2} + 2 a b^{2} = a b^{2}$

查看试题解析
4. 方程 $\frac{2 x - 1}{2} - \frac{x + 1}{3} = 1$ ，去分母，得（）

A、 $2 x - 1 - x + 1 = 6$ B、 $3 (2 x - 1) - 2 (x + 1) = 6$ C、 $2 (2 x - 1) - 3 (x + 1) = 6$ D、 $3 x - 3 - 2 x - 2 = 1$

查看试题解析
5. 下列展开图不能折成正方体的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，A、O、B在同一直线上，且 $∠ A O C = ∠ B O C = ∠ E O F = 90 °$ ，则 $∠ A O E$ 的余角有（）

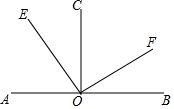A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 用 $7.8$ 米长的铁丝做成一个长方形框架，使长比宽多 $1.2$ 米，求这个长方形框架的宽是多少米？设长方形的宽x米，可列方程为（）

A、 $x + (x + 1.2) = 7.8$ B、 $x + (x - 1.2) = 7.8$ C、 $2 [x + (x + 1.2)] = 7.8$ D、 $2 [x + (x - 1.2)] = 7.8$

查看试题解析
8. 下列说法中正确的是（）

A、画一条3厘米长的射线 B、画一条3厘米长的直线 C、画一条5厘米长的线段 D、在线段、射线、直线中直线最长

查看试题解析
9. 按一定规律排列的一组数： $\frac{1}{2}$ ， $\frac{1}{6}$ ， $\frac{1}{12}$ ， $\frac{1}{20}$ ， $\dots$ ， $\frac{1}{a}$ ， $\frac{1}{90}$ ， $\frac{1}{b} ($ 其中a，b为整数 $)$ ，则 $a + b$ 的值为（）

A、182 B、172 C、242 D、200

查看试题解析
10. 如图，下列四个图形是由已知的四个立体图形展开得到的，则对应的序号是（）

$①$ 圆柱 $②$ 正方体 $③$ 三棱柱 $④$ 四棱锥

A、 $① ② ③ ④$ B、 $② ① ③ ④$ C、 $③ ② ① ④$ D、 $④ ② ① ③$

查看试题解析

二、填空题（本大题共7小题，共28.0分）

11. $A$ 、 $B$ 两地之间弯曲的公路改直，能够缩短路程，其根据的道理是.

查看试题解析
12. 已知 $α = 50 °$ ，则它的余角与补角的度数和等于 $°$ .

查看试题解析
13. 计算： $22^{\circ} 16' \div 4 =$ $69 ° - 23 ° 14' 15 ″ =$ $. ($ 结果用度、分、秒表示 $)$

查看试题解析
14. 如图，射线 $O A$ 表示西北方向，若射线 $O B$ 表示南偏西 $60 °$ 的方向，则锐角 $∠ A O B$ 的大小是度．

查看试题解析
15. 将一块长方形铁皮的四个角各剪去一个边长为2cm的小正方形，做成一个无盖的盒子.已知长方形铁皮的宽为10cm ，盒子的容积为 $300 c m^{3}$ ，则铁皮的长为cm.

查看试题解析
16. 计算： $| \frac{1}{2018} - \frac{1}{2017} | + | \frac{1}{2017} - \frac{1}{2016} | - | \frac{1}{2018} - \frac{1}{2016} | =$ .

查看试题解析
17. 如图， $A B = 12$ ，C为AB的中点，点D在线段AC上，且AD： $D C = 1$ ：2，则 $A D =$ .

查看试题解析

三、解答题（本大题共6小题，共42.0分）

18. 如图，点A、O、B在同一条直线上，∠AOC=∠BOD，OE是∠BOC的平分线.

(1)、若∠AOC=46°，求∠DOE的度数；

(2)、若∠DOE=30°，求∠AOC的度数.

查看试题解析
19. 先化简，再求值： $5 (3 a^{2} b - a b^{2}) - 4 (3 a^{2} b - a b^{2})$ ，其中 $a = \frac{1}{2}$ ， $b = - 4$ .

查看试题解析
20. 解方程

(1)、 $2 (100 - 15 x) = 60 + 5 x$

(2)、 $\frac{2 x - 1}{3} - \frac{10 x + 1}{6} = 1$ .

查看试题解析
21. 某工人安装一批机器，若每天安装4台，预计若干天完成，安装这批机器的 $\frac{2}{3}$ 后，改用新方法安装，工作效率提高到原来的 $1.5$ 倍，因此比预计时间提前一天完工，问：这批机器有多少台？预计几天完成？

查看试题解析
22. 甲骑电瓶车，乙骑自行车从相距17km的两地相向而行.

(1)、甲、乙同时出发经过 $0.5 h$ 相遇，且甲每小时的行程是乙每小时行程的3倍少 $6 k m .$ 求乙骑自行车的速度.

(2)、若甲、乙骑行速度保持与 $(1)$ 中的速度相同，乙先出发 $0.5 h$ ，甲才出发，问甲出发几小时后两人相遇？

查看试题解析
23. 如图，点O在直线AD上， $∠ B O F = ∠ C O D = 90 °$ ，OE平分 $∠ D O F$ .

(1)、图中与 $∠ B O C$ 相等的角是；图中与 $∠ E O F$ 互补的角是.

(2)、若 $∠ E O F = 4 ∠ B O C$ ，求 $∠ B O C$ 和 $∠ C O E$ 的度数.

查看试题解析