辽宁省鞍山市2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-02-23 类型：期末考试

进入出卷网下载

一、选择题（共10小题）.

1. 下面各图形中，对称轴最多的是（）

A、长方形 B、正方形 C、等边三角形 D、等腰三角形

查看试题解析
2. 已知图中的两个三角形全等，则∠α的度数是（）

A、72° B、60° C、58° D、50°

查看试题解析
3. 下列运算正确的是（）

A、a³•a⁴＝a¹² B、（m³）²＝m⁵ C、x³+x³＝x⁶ D、（﹣a²）³＝﹣a⁶

查看试题解析
4. 如图，△ABC中，AB＝AC，D是BC中点，下列结论中不正确的是（）

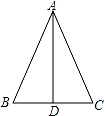A、∠B＝∠C B、AD⊥BC C、AD平分∠BAC D、AB＝2BD

查看试题解析
5. 下列各分式中，最简分式是（）

A、 $\frac{x^{2} + y^{2}}{x + y}$ B、 $\frac{x^{2} - y^{2}}{x - y}$ C、 $\frac{x^{2} - y^{2}}{{(x + y)}^{2}}$ D、 $\frac{2 x + 2 y}{6 x - 6 y}$

查看试题解析
6. 下列因式分解正确的是（）

A、﹣3x²ⁿ﹣6xⁿ＝﹣3xⁿ（x²+2） B、x²+x+1＝（x+1）² C、2x²﹣ $\frac{1}{2}$ ＝2（x+ $\frac{1}{2}$ ）（x﹣ $\frac{1}{2}$ ） D、4x²﹣16＝（2x+4）（2x﹣4）

查看试题解析
7. 如图，在△ABC中，∠B＝55°，∠C＝30°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（）

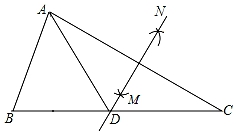A、65° B、60° C、55° D、45°

查看试题解析
8. 如图，Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点D作DF⊥AB，垂足为点F，点E在边AC上，若DE＝DB，则下列结论不正确的是（）

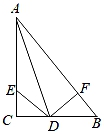A、DC＝DF B、DE＝BF C、AC＝AF D、AB＝AC+CE

查看试题解析
9. 在平面直角坐标系中，点A，B的坐标分别为（﹣3，0）、（0，﹣5），若平面内存在一点C，使△ABC是等腰直角三角形，则下列C点坐标错误的是（）

A、（﹣8，﹣3） B、（﹣5，﹣8） C、（2，3） D、（5，﹣3）

查看试题解析

二、填空题（共8小题）.

10. （﹣ $\frac{2}{3}$ ）²⁰²⁰•（1.5）²⁰²¹＝.

查看试题解析
11. 已知△ABC的两条边长分别为2和5，则第三边c的取值范围是.

查看试题解析
12. 如图，△ABC中，CD平分∠ACB，若∠A＝68°，∠BCD＝31°，则∠B＝.

查看试题解析
13. 若一个多边形外角和与内角和相等，则这个多边形是边形．

查看试题解析
14. 已知x+y＝6，xy＝7，则x²y+xy²的值是.

查看试题解析
15. 甲、乙两个港口之间的海上行程为skm，一艘轮船以akm/h的航速从甲港顺水航行到达乙港.已知水流速度为xkm/h，则这艘轮船从乙港逆水航行回到甲港所用的时间为h.

查看试题解析
16. 如图的4×4的正方形网格中，有A，B，C，D四点，直线a上求一点P，使PA+PB最短，则点P应选点（C或D）.

查看试题解析
17. 如图，在△ABC中，若∠ABC＝45°，P为BC边上一点，且PC＝2PB，∠APC＝60°，过点C作CE⊥AP，则∠ACB的度数是.

查看试题解析

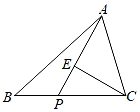
三、解答题：（本题共44分）

18. 计算：

(1)、4xy²z÷（﹣2x^﹣2yz^﹣1）²；

(2)、（m+2+ $\frac{5}{2 - m}$ ）• $\frac{2 m - 4}{3 - m}$ .

查看试题解析
19. 先化简，再求值：
（a²b﹣2ab﹣b²）÷b﹣（a+b）（a﹣b），其中a＝0.5，b＝﹣1.

查看试题解析
20. 如图，在等腰直角三角形ABC中，∠ACB＝90°，点M是边AB上任意一点，连接CM，过点A，B分别作AE⊥CM，BF⊥CM，垂足分别为E，F，若BF＝2.6cm，AE＝0.9cm，分别求出CF，EF的长.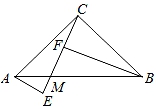

查看试题解析
21. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和点M.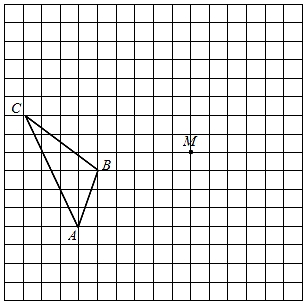

（ 1 ）在给出图上画出一个格点△MB₁C₁ ，并使它与△ABC全等且A与M是对应点；

（ 2 ）以点M所在的水平直线为对称轴，画出△ABC的轴对称图形△A₂B₂C₂.

查看试题解析
22. 观察下列各式：
1²+3²+4²＝2×（1²+3²+3）

2²+3²+5²＝2×（2²+3²+6）

3²+6²+9²＝2×（3²+6²+18）

…

(1)、请用a，b，c表示左边由小到大的三个底数，并写出它们之间的关系；

(2)、请用字母a，b写出上述等式的规律，并加以证明.

查看试题解析

四、综合题：（本题共20分）

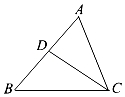
23. 假期里，学校组织部分团员同学参加“关爱老年人”的爱心援助活动，计划分乘大、小两辆车前往相距140km的乡村敬老院.

(1)、若小车速度是大车速度的1.4倍，则小车比大车早一个小时到达，求大、小车速度.

(2)、若小车与大车同时以相同速度出发，但走了60千米以后，发现有物品遗忘，小车准备加速返回取物品，要想与大车同时到达，应提速到原来的多少倍？

查看试题解析
24. 如图，在△ABC中.

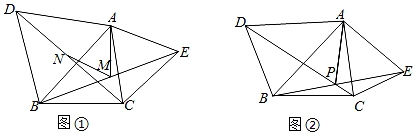(1)、如图①，分别以AB、AC为边作等边△ABD和等边△ACE，连接BE，CD；
①猜想BE与CD的数量关系是 ▲ ；

②若点M，N分别是BE和CD的中点，求∠AMN的度数；

(2)、如图②，若分别以AB、AC为边作△ABD和△ACE，且AD＝AB，AC＝AE，∠DAB＝∠CAE＝α，DC、BE交于点P，连接AP，请直请接写出∠APC与α的数量关系

查看试题解析