辽宁省抚顺市抚顺县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-02-23 类型:期末考试
一、单选题
-
1. 下列各组中的两个图形属于全等图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一种花瓣的花粉颗粒直径用科学记数法表示为 ,这个数用小数表示为( )A、0.00065 B、0.000065 C、0.0000065 D、0.000000653. 四组木条(每组 根)的长度分别如图,其中能组成三角形的一组是( )A、
2. 一种花瓣的花粉颗粒直径用科学记数法表示为 ,这个数用小数表示为( )A、0.00065 B、0.000065 C、0.0000065 D、0.000000653. 四组木条(每组 根)的长度分别如图,其中能组成三角形的一组是( )A、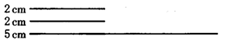 B、
B、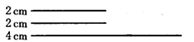 C、
C、 D、
D、 4. 下列运算的结果为a6的是A、 B、 C、 D、5. 我国建造的港珠澳大桥全长55公里,集桥、岛、隧于一体,是世界最长的跨海大桥.如图,这是港珠澳大桥中的斜拉索桥,那么你能推断出斜拉索大桥中运用的数学原理是( )
4. 下列运算的结果为a6的是A、 B、 C、 D、5. 我国建造的港珠澳大桥全长55公里,集桥、岛、隧于一体,是世界最长的跨海大桥.如图,这是港珠澳大桥中的斜拉索桥,那么你能推断出斜拉索大桥中运用的数学原理是( ) A、三角形的不稳定性 B、三角形的稳定性 C、四边形的不稳定性 D、四边形的稳定性6. 下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是( )A、
A、三角形的不稳定性 B、三角形的稳定性 C、四边形的不稳定性 D、四边形的稳定性6. 下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 下列从左到右的变形,错误的是( )A、 B、 C、 D、8. 如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是( )
7. 下列从左到右的变形,错误的是( )A、 B、 C、 D、8. 如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是( )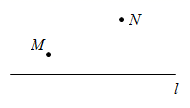 A、
A、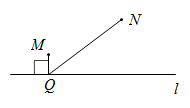 B、
B、 C、
C、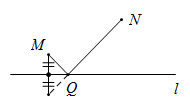 D、
D、 9. 某施工队承接了60公里的修路任务,为了提前完成任务,实际每天的工作效率比原计划提高了25%,结果提前60天完成了这项任务.设原计划每天修路 公里,根据题意列出的方程正确的是( )A、 B、 C、 D、10. 如图所示,有三条道路围成Rt△ABC,其中BC=1000m,一个人从B处出发沿着BC行走了800m,到达D处,AD恰为∠CAB的平分线,则此时这个人到AB的最短距离为( )
9. 某施工队承接了60公里的修路任务,为了提前完成任务,实际每天的工作效率比原计划提高了25%,结果提前60天完成了这项任务.设原计划每天修路 公里,根据题意列出的方程正确的是( )A、 B、 C、 D、10. 如图所示,有三条道路围成Rt△ABC,其中BC=1000m,一个人从B处出发沿着BC行走了800m,到达D处,AD恰为∠CAB的平分线,则此时这个人到AB的最短距离为( ) A、1000m B、800m C、200m D、1800m
A、1000m B、800m C、200m D、1800m二、填空题
-
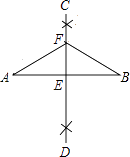
11. 在 , , 这3个效中,最大的数是.12. 一个正n边形的每一外角都等于60°,则n的值是.13. 若分式 有意义,则x满足的条件是.14. 计算: .15. 如图,已知线段AB,分别以点A和点B为圆心,大于 AB的长为半径作弧,两弧相交于C,D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB= .
 16. 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,则DE长为.
16. 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,则DE长为. 17. 如图,AB=AD,要证明△ABC与△ADC全等,只需增加的一个条件是
17. 如图,AB=AD,要证明△ABC与△ADC全等,只需增加的一个条件是
三、解答题
-
18. 如图,∠MON=30°,点A1 、A2 、A3 、A4 …在射线ON上,点B1 、B2 、B3 …在射线OM上,△A 1B1A2 、△A2B2A3 、△A3B3A4 …均为等边三角形,若OA1 =1,则△A6B6A7的边长为 .
 19.(1)、分解因式:(2)、计算:20.(1)、计算:(2)、解方程:21. 如图,在平面直角坐标系中, 、 、 .
19.(1)、分解因式:(2)、计算:20.(1)、计算:(2)、解方程:21. 如图,在平面直角坐标系中, 、 、 . (1)、在图中作出 关于y轴的对称图形 ,并写出点 的坐标;(2)、请直接写出 的面积;(3)、若点 与点 关于x轴对称,请直接写出m、n的值.22. 如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区城进行绿化,空白区城进行广场硬化,阴影部分是边长为(a+b)米的正方形.
(1)、在图中作出 关于y轴的对称图形 ,并写出点 的坐标;(2)、请直接写出 的面积;(3)、若点 与点 关于x轴对称,请直接写出m、n的值.22. 如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区城进行绿化,空白区城进行广场硬化,阴影部分是边长为(a+b)米的正方形. (1)、计算广场上需要硬化部分的面积;(2)、若a=30,b=10,求硬化部分的面积.23. 中 , ,点P在BC边上运动(P不与B.C重合),连接AP,作 ,PQ交AB于点Q.
(1)、计算广场上需要硬化部分的面积;(2)、若a=30,b=10,求硬化部分的面积.23. 中 , ,点P在BC边上运动(P不与B.C重合),连接AP,作 ,PQ交AB于点Q. (1)、如图1,当 时,判断 的形状并说明理由;(2)、在点P的运动过程中, 的形状可以是等腰三角形吗?若可以,请直接写出 的度数;若不可以,请说明理由.24. 列方程解应用题:
(1)、如图1,当 时,判断 的形状并说明理由;(2)、在点P的运动过程中, 的形状可以是等腰三角形吗?若可以,请直接写出 的度数;若不可以,请说明理由.24. 列方程解应用题:中华优秀传统文化是中华民族的“根”和“魂”.为传承优秀传统文化,某校购进《西游记》和《三国演义》若干套,其中每套《西游记》的价格比每套《三国演义》的价格多40元,用3200元购买《三国演义》的套数是用2400元购买《西游记》套数的2倍,求每套《三国演义》的价格.
25. 已知 是等腰直角三角形, , .直角顶点C在x轴上,锐角顶点B在y轴上,过点A作 轴,垂足为点D.当点B不动,点C在x轴上滑动的过程中.

 (1)、如图1,当点C的坐标是 ,点A的坐标是 时,请求出点B的坐标;(2)、如图2,当点C的坐标是 时,请写出点A的坐标;(3)、如图3,过点A作直线 轴,交y轴于点E,交BC延长线于点F.AC与y轴交于点G.当y轴恰好平分 时,请写出AE与BG的数量关系.26. 已知 中, ; 中, ; ,点A.D.E在同一直线上,AE与BC相交于点F,连接BE.
(1)、如图1,当点C的坐标是 ,点A的坐标是 时,请求出点B的坐标;(2)、如图2,当点C的坐标是 时,请写出点A的坐标;(3)、如图3,过点A作直线 轴,交y轴于点E,交BC延长线于点F.AC与y轴交于点G.当y轴恰好平分 时,请写出AE与BG的数量关系.26. 已知 中, ; 中, ; ,点A.D.E在同一直线上,AE与BC相交于点F,连接BE. (1)、如图1,当 时,
(1)、如图1,当 时,①请直接写出 和 的形状;
②求证: ;
③请求出 的度数.
(2)、如图2,当 时,请直接写出:① 的度数;
②若 , ,线段AF的长.