湖北省武汉市武昌区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-02-23 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分）

1. 下列交通标志中，成轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{x}{3 x + 4}$ 的值为1，则x的值是（）

A、1 B、2 C、-1 D、-2

查看试题解析
3. 下列计算正确的是（）

A、 $m^{6} \cdot m^{2} = m^{12}$ B、 $m^{6} \div m^{2} = m^{3}$ C、 ${(\frac{a}{b})}^{5} = \frac{a}{b}$ D、 ${(m^{3})}^{2} = m^{6}$

查看试题解析
4. 如图所示是两个全等三角形，由图中条件可知， $∠ α = （）$

A、 $65 °$ B、 $30 °$ C、 $85 °$ D、 $30 °$ 或 $65 °$

查看试题解析
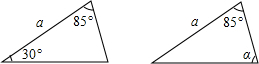5. 0.000000035米用科学记数法表示为（）

A、 $3.5 \times 10^{- 8}$ 米 B、 $3.5 \times 10^{- 9}$ 米 C、 $35 \times 10^{- 9}$ 米 D、 $3.5 \times 10^{- 10}$ 米

查看试题解析
6. 下列计算正确的是（）

A、 $(a + 3 b) (a - 3 b) = a^{2} - 3 b^{2}$ B、 $(- a + 3 b) (a - 3 b) = - a^{2} - 9 b^{2}$ C、 $(a - 3 b) (a - 3 b) = a^{2} - 9 b^{2}$ D、 $(- a - 3 b) (- a + 3 b) = a^{2} - 9 b^{2}$

查看试题解析
7. 在等腰三角形ABC中， $∠ A$ 与 $∠ B$ 的度数之比为 $5 : 2$ ，则 $∠ A$ 的度数是（）

A、 $100 °$ B、 $75 °$ C、 $150 °$ D、 $75 °$ 或 $100 °$

查看试题解析
8. 下列变形正确的是（）

A、 $x^{3} - x^{2} - x = x (x^{2} - x)$ B、 $x^{2} - 3 x + 2 = x (x - 3) - 2$ C、 $a^{2} - 9 = (a + 3) (a - 3)$ D、 $a^{2} - 4 a + 4 = {(a + 2)}^{2}$

查看试题解析
9. 如图，已知： $∠ M O N = 30 °$ ，点 $A_{1}$ 、 $A_{2}$ 、 $A_{3 -} \dots \dots$ 在射线ON上，点 $B_{1}$ 、 $B_{2}$ 、 $B_{3} \dots \dots$ 在射线OM上， $△ A_{1} B_{1} A_{2}$ 、 $△ A_{2} B_{2} A_{3}$ 、 $△ A_{3} B_{3} A_{4} \dots \dots$ 均为等边三角形，若 $O A_{1} = 1$ ，则 $△ A_{2018} B_{2018} A_{2019}$ 的边长为（）

A、2017 B、2018 C、 $2^{2017}$ D、 $2^{2018}$

查看试题解析
10. 如图， $△ A B C$ 是等边三角形， $△ A C D$ 是等腰直角三角形， $∠ A C D = 90 °$ ，连接BD，则 $∠ C B D$ 的度数为（）

A、 $10 °$ B、 $15 °$ C、 $20 °$ D、 $25 °$

查看试题解析

二、填空题（本大题共6小题，共18.0分）

11. 要使分式 $\frac{3}{x - 1}$ 有意义，则x的取值范围是.

查看试题解析
12. 在正n边形中，若一个内角等于一个外角的3倍，则边数n的值是.

查看试题解析
13. 已知 $m + n = 12$ ， $m - n = 2$ ，则 $m^{2} - n^{2} =$ .

查看试题解析
14. 如图， $△ A B C$ 中， $A B = A C$ ， $∠ A = 40 °$ ，MN垂直平分AB，则 $∠ N B C =$ .

查看试题解析
15. 如图，OP平分 $∠ A O B$ ， $P B ⊥ O B$ ， $O A = 8 c m$ ， $P B = 3 c m$ ，则 $△ P O A$ 的面积等于.

查看试题解析
16. 在 $△ A B C$ 中， $A B = 8$ ， $A C = 5$ ， $∠ A B C = 30 °$ ，则 $B C =$ .

查看试题解析

三、计算题（本大题共1小题，共8.0分）

17. 解分式方程：

(1)、 $\frac{40}{x - 3} = \frac{64}{x}$ ；

(2)、 $\frac{2 x}{x - 1} + 2 = \frac{- 2}{1 - x}$ .

查看试题解析

四、解答题（本大题共7小题，共64.0分）

18. 因式分解：

(1)、 $4 x^{2} - 8 x y + 2 x$

(2)、 $3 x (a - b) - 6 y (b - a)$

(3)、 $2 a^{3} - 8 a$

(4)、 ${(x^{2} + 4)}^{2} - 16 x^{2}$

查看试题解析
19. 如图，点A，B，C，D在一条直线上，且 $A B = C D$ ，若 $∠ 1 = ∠ 2$ ， $E C = F B .$ 求证： $∠ E = ∠ F$ .

查看试题解析
20. 先化简，再求值： $(1 - \frac{1}{x + 1}) \div \frac{x - 2}{x + 1}$ ，其中 $x = - 4$ .

查看试题解析
21. 如图， $△ A B C$ 在平面直角坐标系中的坐标分别为 $A (- 3 ， 4)$ ， $B (- 6 ， 2)$ ， $C (- 2 ， - 2)$

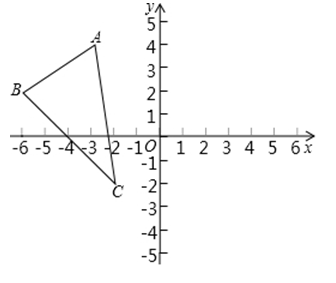(1)、作出 $△ A B C$ 关于y轴对称的图形 $△ A_{1} B_{1} C_{1}$ ；

(2)、分别求出 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的坐标.

查看试题解析
22. 某公司购买了一批A、B型芯片，其中A型芯片的单价比B型芯片的单价少9元，已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.

(1)、求该公司购买的A、B型芯片的单价各是多少元？

(2)、若两种芯片共购买了200条，且购买的总费用不超过6300元，求A型芯片至少购买多少条？

查看试题解析
23. 已知：如图，在平面直角坐标系中， $∠ O A C = ∠ O C A = 60 °$ ， $O C = C B$

(1)、如图①，若 $O B = 8$ ，求点A的坐标

(2)、点E为线段AB上一动点，点E的横坐标为t， $∠ E O F = 60 °$ ， $E O = F O$ ，连接BF，①如图②在（1）的条件下，设 $△ O F B$ 的面积为S，请用含t的式子表示S，②如图③，连接EF，EF交射线AC于点N，若 $∠ E N A = 45 °$ ， $E N = 3 \sqrt{2}$ ，求点E的坐标.

查看试题解析
24. 如图 $①$ ，在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ，点D是AC的中点，连接BD，过点C作CE平分 $∠ A C B$ 交BD于点E，点F在AB上，且 $∠ A C F = ∠ C B D$

(1)、求证： $C F = B E$ ；

(2)、如图②，过点A作 $A G ⊥ A B$ 交BD的延长线于点G，
①若 $D G = 2$ ，求CF；

②设CF交BD于H，求 $\frac{H E}{A G}$ 的值.

查看试题解析