湖北省十堰市丹江口市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-02-23 类型:期末考试
一、选择题(本大题共10小题,共30.0分)
-
1. 下列各图中,不是轴对称图形的是( )A、
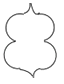 B、
B、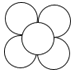 C、
C、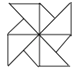 D、
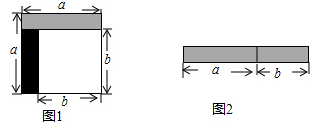
D、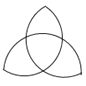 2. 已知点M与点 关于x轴对称,那么点M的坐标为( )A、 B、 C、 D、3. 使分式 有意义的x的取值是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 下列各式从左到右的变形是因式分解的是( )A、 B、 C、 D、6. 下列式子中是最简二次根式的是( )A、 B、 C、 D、7. 从边长为a的正方形中剪掉一个边长为b的正方形 如图1所示 ,然后将剩余部分拼成一个长方形 如图2所示 根据图形的变化过程,写出的一个正确的等式是( )
2. 已知点M与点 关于x轴对称,那么点M的坐标为( )A、 B、 C、 D、3. 使分式 有意义的x的取值是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 下列各式从左到右的变形是因式分解的是( )A、 B、 C、 D、6. 下列式子中是最简二次根式的是( )A、 B、 C、 D、7. 从边长为a的正方形中剪掉一个边长为b的正方形 如图1所示 ,然后将剩余部分拼成一个长方形 如图2所示 根据图形的变化过程,写出的一个正确的等式是( )
 A、 B、 C、 D、8. 如图,用直尺和圆规作一个角
A、 B、 C、 D、8. 如图,用直尺和圆规作一个角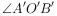 ,等于已知角 ,能得出
,等于已知角 ,能得出  的依据是( )
的依据是( )
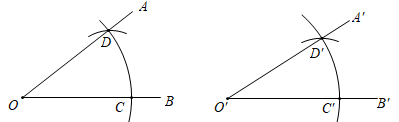 A、SAS B、ASA C、AAS D、SSS9. 下列各式从左到右的变形正确的是( )A、 = B、 C、 D、10. 如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长( )
A、SAS B、ASA C、AAS D、SSS9. 下列各式从左到右的变形正确的是( )A、 = B、 C、 D、10. 如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长( )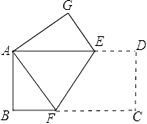 A、3 B、4 C、3.5 D、6
A、3 B、4 C、3.5 D、6二、填空题(本大题共4小题,共12.0分)
-
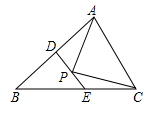
11. 随着人们对环境的重视,新能源的开发迫在眉睫,石墨烯是现在世界上最薄的纳米材料,其理论厚度应是 ,用科学记数法表示是m.12. 要使 有意义,则x的取值范围为.13. 已知 是一个关于x的完全平方式,则常数n的值为。14. 如图,在 中, , ,AB的垂直平分线DE交AB边于点D,交BC边于点E,在线段DE上有一动点P,连接AP、PC,则 的周长最小值为.
三、解答题(本大题共10小题,共80.0分)
-
15. 计算: .16. 计算:(1)、(2)、17. 解下列各题:(1)、分解因式: ;(2)、甲,乙两同学分解因式 ,甲看错了n,分解结果为 ;乙看错了m,分解结果为 ,请分析一下m,n的值及正确的分解过程.18. 如图, 三个顶点的坐标分别为 , , ,
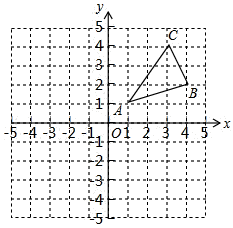
( 1 )画出 关于y轴的对称图形 ,并写出点 的坐标;
( 2 )在x轴上求作一点P,使 的周长最小,并直接写出点P的坐标.
19. 如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D,使 过点D作 ,且A,C,E三点在一直线上.若测得 米,即可知道AB也为15米.请说明理由. 20. 先化简,再求值: ,其中 .21. 阅读下面材料,回答问题:(1)、在化简 的过程中,小张和小李的化简结果不同;
20. 先化简,再求值: ,其中 .21. 阅读下面材料,回答问题:(1)、在化简 的过程中,小张和小李的化简结果不同;小张的化简如下: = = =
小李的化简如下: = = =
请判断谁的化简结果是正确的,谁的化简结果是错误的,并说明理由.
(2)、请你利用上面所学的方法化简:① ;② .22. 甲、乙两人分别从距离目的地6千米和10千米的两地同时出发,甲、乙的速度比是3:4,结果甲比乙提前20分钟到达目的地,求甲、乙的速度.23. 已知 和 为等腰三角形, , , ,点E在AB上,点F在射线AC上. (1)、如图1,若 ,点F与点C重合,
(1)、如图1,若 ,点F与点C重合,①求证: ;
②求证: .
(2)、如图2,若 ,那么线段AF,AE,BC之间存在怎样的数量关系.24. 如图 在平面直角坐标系中,已知点 , 的坐标满足 连接 点C在x轴负半轴上,作AH垂直BC交BC于点H,交OB于点P,且 .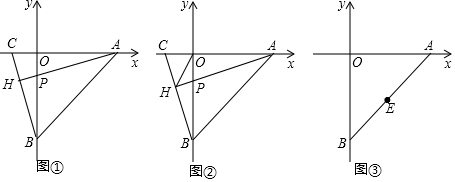 (1)、直接写出点A与点B的坐标:(2)、如图②,在题(1)的条件下,连接OH,求证: ;(3)、如图③,E为AB的中点,动点G在y轴上,连接GE,作 交x轴于F,猜想GB,OB,AF三条线段之间的数量关系,并说明理由.
(1)、直接写出点A与点B的坐标:(2)、如图②,在题(1)的条件下,连接OH,求证: ;(3)、如图③,E为AB的中点,动点G在y轴上,连接GE,作 交x轴于F,猜想GB,OB,AF三条线段之间的数量关系,并说明理由.