河南省南阳市方城县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-02-23 类型:期末考试
一、选择题(本大题共10小题,共30.0分)
-
1. 下列4个数: , ,π,0,其中无理数是( )A、 B、 C、 D、02. 下列计算结果正确的是( )A、 B、 C、 D、3. 下列条件中,不能判断一个三角形是直角三角形的是( )A、三条边的比为 B、三条边满足关系 C、三条边的比为 D、三个角满足关系4. 下列命题是真命题的是( )A、同旁内角互补 B、三角形的一个外角大于内角 C、三角形的一个外角等于它的两个内角之和 D、直角三角形的两锐角互余5. 分解因式 结果正确的是( )A、 B、 C、 D、6. 如图,AD、BC相交于点O, , ,下列结论中,错误的是( )
 A、 B、 C、 D、7. “救死扶伤”是我国的传统美德,某媒体就“老人摔倒该不该扶”进行了调查,将得到的数据经统计分析后绘制成如图所示的扇形统计图,根据统计图判断下列说法,其中错误的一项是( )
A、 B、 C、 D、7. “救死扶伤”是我国的传统美德,某媒体就“老人摔倒该不该扶”进行了调查,将得到的数据经统计分析后绘制成如图所示的扇形统计图,根据统计图判断下列说法,其中错误的一项是( ) A、认为依情况而定的占27% B、认为该扶的在统计图中所对应的圆心角是234° C、认为不该扶的占8% D、认为该扶的占92%8. 如图, 是 上一点, 交 于点 , , ,若 , ,则 的长是( )
A、认为依情况而定的占27% B、认为该扶的在统计图中所对应的圆心角是234° C、认为不该扶的占8% D、认为该扶的占92%8. 如图, 是 上一点, 交 于点 , , ,若 , ,则 的长是( ) A、0.5 B、1 C、1.5 D、29. 如图,在 中, , 的垂直平分线DE分别交AB,BC于点D,E,则 的度数为( )
A、0.5 B、1 C、1.5 D、29. 如图,在 中, , 的垂直平分线DE分别交AB,BC于点D,E,则 的度数为( ) A、 B、 C、 D、10. 如图, ,MQ为 的角平分线.若 ,则 的度数是( )
A、 B、 C、 D、10. 如图, ,MQ为 的角平分线.若 ,则 的度数是( )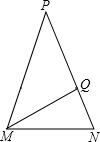 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5小题,共15.0分)
-
11. 的平方根是 .12. 如图,将 绕直角顶点C顺时针旋转 ,得到 ,连结 ,若 ,则 的度数是.
 13. 某校规定学生的学期数学成绩满分为100分,其中平时成绩占30%,期末卷面成绩占70%.小李的平时成绩、期末卷面成绩(百分制)依次为90分、85分,则小李本学期的数学成绩是分.14. 如图所示,已知四边形ABCD中, , , , ,且 求四边形ABCD的面积 .
13. 某校规定学生的学期数学成绩满分为100分,其中平时成绩占30%,期末卷面成绩占70%.小李的平时成绩、期末卷面成绩(百分制)依次为90分、85分,则小李本学期的数学成绩是分.14. 如图所示,已知四边形ABCD中, , , , ,且 求四边形ABCD的面积 . 15. 如图,一张矩形纸片ABCD,沿AF折叠,点B恰好落在CD边上的点E处,已知CD为10cm , DE: :2,则FC的长度为 cm.
15. 如图,一张矩形纸片ABCD,沿AF折叠,点B恰好落在CD边上的点E处,已知CD为10cm , DE: :2,则FC的长度为 cm.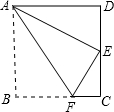
三、解答题(本大题共8小题,共75.0分)
-
16. 计算:(1)、(2)、17. 如图,在 中, .
 (1)、用尺规作图法作 的平分线BD,交AC于点 保留作图痕迹,不要求写作法和证明 ;(2)、若 ,求BC.18. 先化简,再求值: ,其中 , .19. 已知AC与BD相交于点O,且O是BD的中点, 说明 ≌
(1)、用尺规作图法作 的平分线BD,交AC于点 保留作图痕迹,不要求写作法和证明 ;(2)、若 ,求BC.18. 先化简,再求值: ,其中 , .19. 已知AC与BD相交于点O,且O是BD的中点, 说明 ≌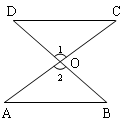 20. 为了加强学生课外阅读,开阔视野,某校开展了“书香校园,诵读经典”活动,学校随机抽查了部分学生,对他们每天的课外阅读时间进行调查,并将调查统计的结果分为四类:每天诵读时间 分钟的学生记为A类,20分钟 分钟记为B类,40分钟 分钟记为C类, 分钟记为D类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
20. 为了加强学生课外阅读,开阔视野,某校开展了“书香校园,诵读经典”活动,学校随机抽查了部分学生,对他们每天的课外阅读时间进行调查,并将调查统计的结果分为四类:每天诵读时间 分钟的学生记为A类,20分钟 分钟记为B类,40分钟 分钟记为C类, 分钟记为D类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题: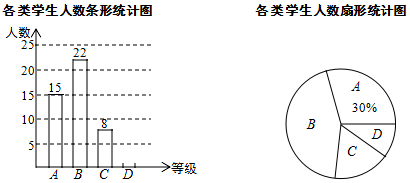 (1)、这次共抽取了名学生进行调查统计,扇形统计图中 类所对应的扇形圆心角大小为;(2)、将条形统计图补充完整;(3)、如果该校共有2000名学生,请你估计该校 类学生约有多少人?21. 如图,在 中, ,点D是AB边上的一点, ,且 ,过点M作 交AB于点 求证: .
(1)、这次共抽取了名学生进行调查统计,扇形统计图中 类所对应的扇形圆心角大小为;(2)、将条形统计图补充完整;(3)、如果该校共有2000名学生,请你估计该校 类学生约有多少人?21. 如图,在 中, ,点D是AB边上的一点, ,且 ,过点M作 交AB于点 求证: . 22. 阅读材料:基本不等式 ,当且仅当 时,等号成立.其中我们把 叫做正数a、b的算术平均数, 叫做正数a、b的几何平均数,它是解决最大 小 值问题的有力工具.
22. 阅读材料:基本不等式 ,当且仅当 时,等号成立.其中我们把 叫做正数a、b的算术平均数, 叫做正数a、b的几何平均数,它是解决最大 小 值问题的有力工具.例如:在 的条件下,当x为何值时, 有最小值,最小值是多少?
解 ,
,即是
,
当且仅当 时,即 时, 有最小值,最小值为2.
请根据阅读材料解答下列问题:
(1)、若 ,函数 ,当x为何值时,函数有最值,并求出其最值,(2)、当 时,式子 成立吗?请说明理由.23. 如图 (1)、如图1, 中, ,求证: ;(2)、如图2, 中, , , , ,垂足分别为D、E,CD与AE交于点 试探究线段AF与线段CE的数量关系.(3)、如图3, 中, , ,垂足为D,若线段 ,则 的面积为.
(1)、如图1, 中, ,求证: ;(2)、如图2, 中, , , , ,垂足分别为D、E,CD与AE交于点 试探究线段AF与线段CE的数量关系.(3)、如图3, 中, , ,垂足为D,若线段 ,则 的面积为.